题目内容
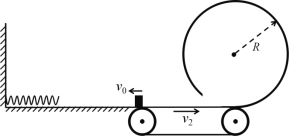
【题目】如图所示，水平面右端放一质量m=0.1kg小物块，给小物块一v0=4m/s的初速度使其向左运动，运动d=1m后将弹簧压至最紧，反弹回到出发点时物块速度大小v1=2m/s．若水平面与一长L=3m的水平传送带平滑连接，传送带以v2=10m/s的速度顺时针匀速转动。传送带右端又与一竖直平面内的光滑圆轨道的底端平滑连接，圆轨道半径R=0.8m．当小物块进入圆轨道时会触发闭合装置将圆轨道封闭。（g=10m/s2，sin 53°＝0.8，cos 53°＝0.6）求：
（1）小物块与水平面间的动摩擦因数
；
（2）要使小物块进入竖直圆轨道后不脱离圆轨道，传送带与物体间的动摩擦因数
应满足的条件。
【答案】（1）
（2）
【解析】
(1)小物块在水平面向左运动再返回的过程，根据能量守恒定律得：
代入数据解得：
(2)设物块在圆轨道最低点时速度为
时，恰好到达圆心右侧等高点。
根据机械能守恒得：
解得：
说明物块在传送带上一直做匀加速运动
由动能定理得：
解得：
设物块在圆轨道最低点时速度为
时，恰好到达圆轨道最高点，
在圆轨道最高点有：
从圆轨道最低点到最高点的过程，由机械能守恒定律得：
解得：
说明物块在传送带上一直做匀加速运动
由动能定理得：
解得：
所以要使物块进入竖直圆轨道后不脱离圆轨道，传送带与物体间的动摩擦因数
应满足的条件是
或
练习册系列答案
相关题目
