题目内容
 如图所示,a、b两块足够长的平板玻璃砖平行放置,且折射率na>nb>
如图所示,a、b两块足够长的平板玻璃砖平行放置,且折射率na>nb>| 2 |
分析:光线通过玻璃砖再进入空气发生两次折射:第一次是从空气斜射进入玻璃砖,折射光线应该靠近法线偏折,折射角小于入射角;第二次是从玻璃砖斜射进入空气,折射光线应该远离法线偏折,折射角大于入射角.由于玻璃砖上下表面垂直,第二次折射的入射角等于第一次折射的折射角,所以第二次折射的折射角等于第一次折射的入射角,最后的出射光线与入射光线BO相比,只是作了平移,出射光线与入射光线平行.三次进入玻璃砖折射后光线仍和第一次的入射光线平行,即可求解.由v=
,比较光在两玻璃砖传播速度的大小.根据光在玻璃砖中传播速度和通过的路程关系,比较光穿透玻璃砖时间的长短.
| c |
| n |
解答:解:
A、光线通过玻璃砖再进入空气发生了两次折射,第二次的入射角等于第一次的折射角,根据光路可逆性原理可知,光不可能在a、b的下表面发生全反射,一定能从下表面射出玻璃砖.故A错误.
B、光线经过玻璃砖时,出射光线与入射光线都平行,通过两块平行玻璃砖后,出射光线与入射光线仍平行.所以从b下表面射出的光线与a上表面的入射光线平行.故B正确.
C、由公式v=
,结合条件折射率na>nb>
,可知,光在a中的速度比光在b中的速度小.故C正确.
D、设a、b两玻璃砖的厚度都是d,入射角为i,根据折射率n=
得,sinr=
,则光线在玻璃砖中通过的路程为S=
,则光通过玻璃砖的时间为:
t=
=
?
=
?
=
?
由上得知,光线在两玻璃砖上表面的入射角i相同,由于折射率na>nb>
,根据折射定律可知,光线在a中折射角小于在b中折射角,且2r<90°,由数学知识得知,光在a中sin2r较小,所以光穿透a的时间大于穿透b的时间.故D正确.
故选BCD
A、光线通过玻璃砖再进入空气发生了两次折射,第二次的入射角等于第一次的折射角,根据光路可逆性原理可知,光不可能在a、b的下表面发生全反射,一定能从下表面射出玻璃砖.故A错误.
B、光线经过玻璃砖时,出射光线与入射光线都平行,通过两块平行玻璃砖后,出射光线与入射光线仍平行.所以从b下表面射出的光线与a上表面的入射光线平行.故B正确.
C、由公式v=
| c |
| n |
| 2 |
D、设a、b两玻璃砖的厚度都是d,入射角为i,根据折射率n=
| sini |
| sinr |
| sini |
| n |
| d |
| cosr |
t=
| S |
| v |
| d |
| cosr |
| n |
| c |
| d |
| cosr |
| sini |
| csinr |
| d |
| c |
| 2sini |
| sin2r |
由上得知,光线在两玻璃砖上表面的入射角i相同,由于折射率na>nb>
| 2 |
故选BCD
点评:本题主要考查光的折射定律:折射光线、入射光线和法线在同一平面内,折射光线、入射光线分居法线两侧,光由空气斜射进入水中或其它透明介质中时,折射光线向法线偏折,折射角小于入射角;光由水或其它透明介质斜射进入空气中时,折射光线远离法线偏折,折射角大于入射角.本题还要注意玻璃砖上下表面平行,玻璃砖两侧的光线就是平行,与折射率无关.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,A、B两块带异号电荷的平行金属板间形成匀强电场,一电子以v0=4×106m/s的速度垂直于场强方向沿中心线由O点射入电场,从电场右侧边缘C点飞出时的速度方向与v0方向成30°的夹角.已知电子电荷大小e=1.6×10-19C,电子质量m=0.91×10-30kg,求:(1)电子在C点时的动能是多少J?
如图所示,A、B两块带异号电荷的平行金属板间形成匀强电场,一电子以v0=4×106m/s的速度垂直于场强方向沿中心线由O点射入电场,从电场右侧边缘C点飞出时的速度方向与v0方向成30°的夹角.已知电子电荷大小e=1.6×10-19C,电子质量m=0.91×10-30kg,求:(1)电子在C点时的动能是多少J? (2009?上海模拟)将某均匀的长方体锯成如图所示的A、B两块后,放在水平桌面上并对齐放在一起,现用垂直于B边的水平力F推物体B,使A、B整体保持矩形并沿力F方向匀速运动,则( )
(2009?上海模拟)将某均匀的长方体锯成如图所示的A、B两块后,放在水平桌面上并对齐放在一起,现用垂直于B边的水平力F推物体B,使A、B整体保持矩形并沿力F方向匀速运动,则( )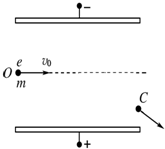 如图所示,A、B两块带等量异号电荷的平行金属板间形成匀强电场,电场强度为E=100N/C,板长为L=2m.一电子以初速度
如图所示,A、B两块带等量异号电荷的平行金属板间形成匀强电场,电场强度为E=100N/C,板长为L=2m.一电子以初速度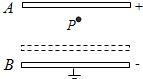 如图所示,A、B两块平行带电金属板,A板带正电,B 板带负电并与地连接,有一带电微粒在两板间P点处静止不动.现将B板上移到虚线处,则P 点的场强
如图所示,A、B两块平行带电金属板,A板带正电,B 板带负电并与地连接,有一带电微粒在两板间P点处静止不动.现将B板上移到虚线处,则P 点的场强