题目内容
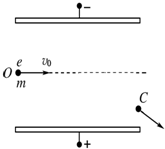 如图所示,A、B两块带等量异号电荷的平行金属板间形成匀强电场,电场强度为E=100N/C,板长为L=2m.一电子以初速度vo=2×106m/s垂直于场强方向沿中心线由O点射入电场,从电场右侧边缘C点飞出电场,.已知电子电荷为e=1.6×10-19C,电子质量m=9.0×10-31Kg.不计电子的重力.求:
如图所示,A、B两块带等量异号电荷的平行金属板间形成匀强电场,电场强度为E=100N/C,板长为L=2m.一电子以初速度vo=2×106m/s垂直于场强方向沿中心线由O点射入电场,从电场右侧边缘C点飞出电场,.已知电子电荷为e=1.6×10-19C,电子质量m=9.0×10-31Kg.不计电子的重力.求:(1)电子在电场中运动的加速度为多少?
(2)电子离开电场时,竖直偏移量为多少?
分析:(1)粒子在电场中做类平抛运动,水平方向是匀速直线运动,竖直方向是匀加速直线运动,根据牛顿第二定律,即可求解;
(2)由竖直方向是匀加速直线运动,根据匀加速运动的位移公式和牛顿第二定律可以求得竖直偏移量的大小.
(2)由竖直方向是匀加速直线运动,根据匀加速运动的位移公式和牛顿第二定律可以求得竖直偏移量的大小.
解答:解:(1)电子在电场中,只受到电场力作用,做类平抛运动,在电场方向做初速度为零的匀加速直线运动.根据牛顿第二定律,则有:
a=
=
=1.8×1013m/s2;
(2)电子在电场方向做匀加速直线运动,根据位移公式,则有:
y=
at2=
×1.8×1013×(
)2m=9m;
答:(1)电子在电场中运动的加速度1.8×1013m/s;
(2)电子离开电场时,竖直偏移量为9m.
a=
| eE |
| m |
| 1.6×10-19×100 |
| 9×10-31 |
(2)电子在电场方向做匀加速直线运动,根据位移公式,则有:
y=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2×106 |
答:(1)电子在电场中运动的加速度1.8×1013m/s;
(2)电子离开电场时,竖直偏移量为9m.
点评:粒子垂直进入电场中做的是类平抛运动,本题就是考查学生对类平抛运动的规律的应用,掌握牛顿第二定律与运动学公式的应用,注意分运动与合运动的等时性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,A、B两块带异号电荷的平行金属板间形成匀强电场,一电子以v0=4×106m/s的速度垂直于场强方向沿中心线由O点射入电场,从电场右侧边缘C点飞出时的速度方向与v0方向成30°的夹角.已知电子电荷大小e=1.6×10-19C,电子质量m=0.91×10-30kg,求:(1)电子在C点时的动能是多少J?
如图所示,A、B两块带异号电荷的平行金属板间形成匀强电场,一电子以v0=4×106m/s的速度垂直于场强方向沿中心线由O点射入电场,从电场右侧边缘C点飞出时的速度方向与v0方向成30°的夹角.已知电子电荷大小e=1.6×10-19C,电子质量m=0.91×10-30kg,求:(1)电子在C点时的动能是多少J? (2009?上海模拟)将某均匀的长方体锯成如图所示的A、B两块后,放在水平桌面上并对齐放在一起,现用垂直于B边的水平力F推物体B,使A、B整体保持矩形并沿力F方向匀速运动,则( )
(2009?上海模拟)将某均匀的长方体锯成如图所示的A、B两块后,放在水平桌面上并对齐放在一起,现用垂直于B边的水平力F推物体B,使A、B整体保持矩形并沿力F方向匀速运动,则( ) 如图所示,a、b两块足够长的平板玻璃砖平行放置,且折射率na>nb>
如图所示,a、b两块足够长的平板玻璃砖平行放置,且折射率na>nb>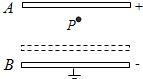 如图所示,A、B两块平行带电金属板,A板带正电,B 板带负电并与地连接,有一带电微粒在两板间P点处静止不动.现将B板上移到虚线处,则P 点的场强
如图所示,A、B两块平行带电金属板,A板带正电,B 板带负电并与地连接,有一带电微粒在两板间P点处静止不动.现将B板上移到虚线处,则P 点的场强