题目内容
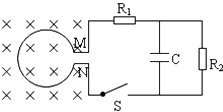
【题目】如图所示，一带电微粒质量为m=2.0×10﹣11kg、电荷量q=+1.0×10﹣5C，从静止开始经电压为U1=100V的电场加速后，从两平行金属板的中间水平进入偏转电场中，微粒从金属板边缘射出电场时的偏转角θ=30°，并接着进入一个方向垂直纸面向里、宽度为D=34.6cm的匀强磁场区域．微粒重力忽略不计．求：
（1）带电微粒进入偏转电场时的速率v1；
（2）偏转电场中两金属板间的电压U2；
（3）为使带电微粒不会由磁场右边射出，该匀强磁场的磁感应强度B至少多大？
【答案】
（1）解：带电微粒经加速电场加速后速率为v1，根据动能定理有U1q= 
mv12
v1= 
=1.0×104m/s．
（2）解：带电微粒在偏转电场中只受电场力作用，
设微粒进入磁场时的速度为v′，则
v′= 
得出v′= 
v1．
由动能定理有
m（v′2﹣v12）=q 
解得：U2=66.7V．
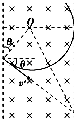
（3）解：带电微粒进入磁场做匀速圆周运动，洛伦兹力提供向心力，微粒恰好不从磁场右边射出时运动轨迹与右边边界相切，设做匀速圆周运动的轨道半径为R，由几何关系知：
R+ 
=D
由牛顿运动定律及运动学规律：
qv′B=m 
，
得B=0.1T．
若带电粒子不射出磁场，磁感应强度B至少为0.1T．
【解析】（1）根据动能定理求带电微粒进入偏转电场时的速率v1；（2）带电微粒在偏转电场中做类平抛运动，将微粒的末速度分解为平行于板和垂直于板两个方向，由几何知识确定出粒子垂直于板方向的末速度，然后由动能定理列式求偏转电压；（3）微粒恰好不从磁场右边射出时运动轨迹与右边边界相切，由几何知识确定运动半径，然后由洛伦兹力提供向心力列方程求磁感应强度的最小值．
【考点精析】关于本题考查的动能定理的综合应用，需要了解应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷才能得出正确答案．
