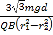题目内容
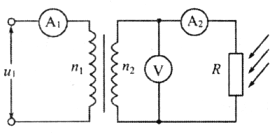
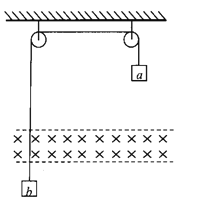
【题目】如图所示,同一竖直面内的正方形导线框a、b的边长均为l,电阻均为R,质量分别为3m和m。它们分别系在一跨过两个定滑轮的绝缘轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面的匀强磁场区域。现将系统由静止释放,当线框b开始进入磁场时,a、b两个线框开始做匀速运动,当线框b刚好完全进入磁场时,线框a刚好开始进入磁场。不计摩擦和空气阻力,重力加速度为g。求:
(1)系统由静止释放时,线框b上边到磁场下边界的距离;
(2)从开始到两线框全部穿过磁场的过程中,共产生的焦耳热Q。
【答案】(1) ![]() ; (2) 8mgl。
; (2) 8mgl。
【解析】
(1)设两线框匀速运动的速度为v,此时轻绳上的张力为T,由平衡条件得:
对a有
T=3mg-BIl
对b有
T=mg
又
![]()
E=Blv
则
![]()
以整体为研究对象,根据牛顿第二定律可得
3mg-mg=4ma
解得
![]()
根据运动学公式可得
v2=2ax
解得
![]()
(2)从开始运动到线框a全部进入磁场的过程中,线框a只在匀速进入磁场的过程中产生焦耳热,设为Q1,由功能关系可得
3mgl-mgl=Q1
所以
Q1=2mgl
从开始到两线框全部穿过磁场的过程中,共产生的焦耳热为
Q=4Q1=8mgl

练习册系列答案
相关题目