题目内容
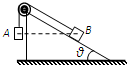 (2012?福建)如图,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好处于静止状态.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物块着地,两物块( )
(2012?福建)如图,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好处于静止状态.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物块着地,两物块( )分析:剪断轻绳后A自由下落,B沿斜面下滑,AB都只有重力做功,机械能守恒,重力势能变化量等于重力所做的功,重力做功的平均功率等于重力做功与时间的比值.
解答:解:设斜面倾角为θ,刚开始AB处于静止状态,所以mBgsinθ=mAg,所以mB>mA,
A、剪断轻绳后A自由下落,B沿斜面下滑,AB都只有重力做功,根据动能定理得:
mv2=mgh
v=
所以速度的变化量为v-0=
,故A错误;
B、剪断细线,A、B两物体都只有重力做功,机械能守恒,则机械能的变化量都为零,故B错误;
C、重力势能变化量△EP=mgh,由于AB的质量不相等,所以重力势能变化不相同,故C错误;
D、A运动的时间为:t1=
,所以A重力做功的平均功率为:
=
B运动有:
=
gsinθt22,解得:t2=
,所以B重力做功的平均功率为:
=
,
而mBgsinθ=mAg,所以重力做功的平均功率相等,故D正确.
故选D
A、剪断轻绳后A自由下落,B沿斜面下滑,AB都只有重力做功,根据动能定理得:
| 1 |
| 2 |
v=
| 2gh |
| 2gh |
B、剪断细线,A、B两物体都只有重力做功,机械能守恒,则机械能的变化量都为零,故B错误;
C、重力势能变化量△EP=mgh,由于AB的质量不相等,所以重力势能变化不相同,故C错误;
D、A运动的时间为:t1=
|
. |
| PA |
| mAgh | ||||
|
B运动有:
| h |
| sinθ |
| 1 |
| 2 |
| 1 |
| sinθ |
|
. |
| PB |
| mBghsinθ | ||||
|
而mBgsinθ=mAg,所以重力做功的平均功率相等,故D正确.
故选D
点评:重力做功决定重力势能的变化与否,若做正功,则重力势能减少;若做负功,则重力势能增加,重力做功的平均功率等于重力做功与时间的比值,难度适中.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 (2012?福建)如图,在点电荷Q产生的电场中,将两个带正电的试探电荷q1、q2分别置于A、B两点,虚线为等势线.取无穷远处为零电势点,若将q1、q2移动到无穷远的过程中外力克服电场力做的功相等,则下列说法正确的是( )
(2012?福建)如图,在点电荷Q产生的电场中,将两个带正电的试探电荷q1、q2分别置于A、B两点,虚线为等势线.取无穷远处为零电势点,若将q1、q2移动到无穷远的过程中外力克服电场力做的功相等,则下列说法正确的是( ) (2012?福建)如图,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5m,离水平地面的高度H=0.8m,物块平抛落地过程水平位移的大小s=0.4m.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2 求:
(2012?福建)如图,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5m,离水平地面的高度H=0.8m,物块平抛落地过程水平位移的大小s=0.4m.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2 求: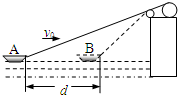 (2012?福建)如图,用跨过光滑定滑轮的缆绳将海面上一艘失去动力的小船沿直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船受到的阻力大小恒为f,经过A点时的速度大小为v0,小船从A点沿直线加速运动到B点经历时间为t1,A、B两点间距离为d,缆绳质量忽略不计.求:
(2012?福建)如图,用跨过光滑定滑轮的缆绳将海面上一艘失去动力的小船沿直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船受到的阻力大小恒为f,经过A点时的速度大小为v0,小船从A点沿直线加速运动到B点经历时间为t1,A、B两点间距离为d,缆绳质量忽略不计.求: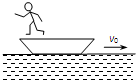 (2012?福建)如图,质量为M的小船在静止水面上以速率v0向右匀速行驶,一质量为m的救生员站在船尾,相对小船静止.若救生员以相对水面速率v水平向左跃入水中,则救生员跃出后小船的速率为 ( )
(2012?福建)如图,质量为M的小船在静止水面上以速率v0向右匀速行驶,一质量为m的救生员站在船尾,相对小船静止.若救生员以相对水面速率v水平向左跃入水中,则救生员跃出后小船的速率为 ( )