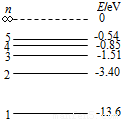题目内容
 (选修模块3-5)
(选修模块3-5)如图所示为氢原子的能级图.用光子能量为13.06eV的光照 射一群处于基态的氢原子,可能观测到氢原子发射的不同波长的光有
10
10
种,其中最短波长为9.5×10-8
9.5×10-8
m(已知普朗克常量h=6.63×10-34 J?s)分析:能级间跃迁吸收会辐射的光子能量等于两能级间的能级差,通过该规律判断基态的氢原子跃迁到第几能级,根据数学组合公式
求出发射不同波长光的种数,能级差越大,辐射的光子频率越大,波长越短,根据能级差,结合Em-En=h
求出最短的波长.
| C | 2 n |
| c |
| λ |
解答:解:因为-13.6+13.06eV=0.54eV,知氢原子跃迁到第5能级,根据
=10,知可能观测到氢原子发射的不同波长的光有10中.
从n=5跃迁到n=1辐射的光子能量最大,波长最短,则△E=h
,即13.06×1.6×10-19=6.63×10-34×
解得λ=9.5×10-8 m.
故答案为:10 9.5×10-8
| C | 2 5 |
从n=5跃迁到n=1辐射的光子能量最大,波长最短,则△E=h
| c |
| λ |
| 3×108 |
| λ |
解得λ=9.5×10-8 m.
故答案为:10 9.5×10-8
点评:解决本题的关键掌握能级间跃迁的特点,知道Em-En=h
.
| c |
| λ |

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 (2010?徐州三模)(选修模块3-5)
(2010?徐州三模)(选修模块3-5)