题目内容
4. 如图所示,水平面上有一个高为d的木块,木块与水平面间的动摩擦因数为μ=0.1.由均匀金属材料制成的边长为2d、有一定电阻的正方形单匝线框,竖直固定在木块上表面,它们的总质量为m.在木块右侧有两处相邻的边长均为2d的正方形区域,正方形底边离水平面高度为2d.两区域各有一水平方向的匀强磁场穿过,其中一个方向垂直于纸面向里,另一个方向垂直于纸面向外,区域Ⅱ中的磁感应强度为区域Ⅰ中的3倍.木块在水平外力作用下匀速通过这两个磁场区域.已知当线框右边MN刚进入Ⅰ区时,外力大小恰好为F0=$\frac{3}{20}$mg,此时M点电势高于N点,试求:
如图所示,水平面上有一个高为d的木块,木块与水平面间的动摩擦因数为μ=0.1.由均匀金属材料制成的边长为2d、有一定电阻的正方形单匝线框,竖直固定在木块上表面,它们的总质量为m.在木块右侧有两处相邻的边长均为2d的正方形区域,正方形底边离水平面高度为2d.两区域各有一水平方向的匀强磁场穿过,其中一个方向垂直于纸面向里,另一个方向垂直于纸面向外,区域Ⅱ中的磁感应强度为区域Ⅰ中的3倍.木块在水平外力作用下匀速通过这两个磁场区域.已知当线框右边MN刚进入Ⅰ区时,外力大小恰好为F0=$\frac{3}{20}$mg,此时M点电势高于N点,试求:(1)区域Ⅰ中磁感应强度的方向如何?
(2)线框右边MN刚进入Ⅰ区时所受安培力大小;
(3)MN刚到达Ⅱ区正中间时,摩擦力的大小;
(4)MN在Ⅱ区运动过程中拉力做的功W?
分析 (1)已知当线框右边MN刚进入Ⅰ区时,M点电势高于N点,说明MN中感应电流方向由N到M,由右手定则判断磁感应强度的方向.
(2)木块和线圈整体水平方向受重力、滑动摩擦力和拉力,根据平衡条件列式求解安培力.
(3)MN刚到达Ⅱ区正中间时,线框左右两边切割磁感线,产生感应电动势,求出总的感应电动势,得到感应电流.由于线框上边各有一半处在磁场Ⅰ区、Ⅱ区中,所以分别受到向上与向下的安培力作用,根据竖直方向力平衡求出地面的支持力,由水平方向力平衡求出拉力F.
(4)随着MN在磁场Ⅱ区的运动,木块受到的支持力Nx随发生的位移x而变化,由平衡条件得到支持力与x的关系,求出支持力的平均值,即可求得摩擦力的平均值,再由功的公式计算拉力做的功W.
解答 解:(1)由题,当线框右边MN刚进入Ⅰ区时,M点电势高于N点,说明MN中感应电流方向由N到M,由右手定则判断知,磁感应强度的方向向外;
(2)线框右边MN刚进入Ⅰ区时,受重力、支持力、拉力、滑动摩擦力和安培力,根据平衡条件,有:
F0-F安-μmg=0
解得:F安=0.05mg
(3)MN刚到达Ⅱ区正中间时,流过线框的电流为:
$I'=\frac{3Bdv+Bdv}{R}=\frac{4Bdv}{R}=4I$
由于线框上边各有一半处在磁场Ⅰ区、Ⅱ区中,所以分别受到向上与向下的安培力作用,此时木块受到的支持力N为:
$N=mg+3BI'd-BI'd=mg+8{F_A}=\frac{7}{5}mg$
故有:f=μN=0.14mg
(4)随着MN在磁场Ⅱ区的运动,木块受到的支持力Nx随发生的位移x而变化,有:
Nx=mg+3BI'x-BI'(2d-x)=mg-2BI'd+4BI'x
由于Nx随位移x线性变化,因此MN在Ⅱ区运动过程中木块受到的平均支持力为:
$\overline N=mg-2BI'd+\frac{4BI'•2d}{2}=mg+2BI'd=\frac{7}{5}mg$
故有:${F_A}'=BI'd+3BI'd=16{F_A}=\frac{4}{5}mg$
此过程中拉力做的功W为:
$W={F_A}'•2d+μ\overline N•2d=\frac{4}{5}mg•2d+\frac{7}{50}mg•2d=\frac{47}{25}mgd$
答:(1)区域Ⅰ中磁感应强度的方向向外;
(2)线框右边MN刚进入Ⅰ区时所受安培力大小为0.05mg;
(3)MN刚到达Ⅱ区正中间时,摩擦力的大小为0.14mg;
(4)MN在Ⅱ区运动过程中拉力做的功W为$\frac{47}{25}mgd$.
点评 本题是电磁感应与电路、力学的综合,关键掌握楞次定律、法拉第电磁感应、欧姆定律等电磁感应的基本规律,要注意线框通过两磁场交界处时左右两边都切割磁感线,产生的感应电动势是串联关系.

 一列波长大于1m的横波沿着x轴正方向传播,处在x1=1m和x2=2m的两质点A、B的振动图象如图所示.由此可知( )
一列波长大于1m的横波沿着x轴正方向传播,处在x1=1m和x2=2m的两质点A、B的振动图象如图所示.由此可知( )| A. | 波长为4m | B. | 波长为$\frac{4}{3}$m | ||
| C. | 1.5s末A、B两质点的速度相同 | D. | 1.5s末A、B两质点的位移大小相等 |
| A. | 子弹克服阻力做的功等于木块动能的增加与摩擦生的热的总和 | |
| B. | 木块对子弹做功的绝对值等于子弹对木块做的功 | |
| C. | 木块对子弹的冲量大小等于子弹对木块的冲量 | |
| D. | 系统损失的机械能等于子弹损失的动能和子弹对木块所做的功的差 |
| A. | $\frac{v}{2g}$ | B. | $\frac{v}{g}$ | C. | $\frac{2v}{g}$ | D. | $\frac{4v}{g}$ |
| A. | 开普勒 | B. | 伽利略 | C. | 牛顿 | D. | 卡文迪许 |
 如图所示,质量为M的木块A上挂一单摆,摆球C质量为m0,它们以相同的速度v0沿光滑水平面运动,与静止放在水平面上的质量为m的木块B发生碰撞.设碰撞时间极短,在此碰撞过程中,如下说法可能发生的是( )
如图所示,质量为M的木块A上挂一单摆,摆球C质量为m0,它们以相同的速度v0沿光滑水平面运动,与静止放在水平面上的质量为m的木块B发生碰撞.设碰撞时间极短,在此碰撞过程中,如下说法可能发生的是( )| A. | A、B、C的速度都发生变化,分别为v1、v2、v3,且满足(M+m0) v0=M v1+m v2+m0 v3 | |
| B. | C的速度不变,A、B的速度变为v,且满足Mv0=(M+m) v | |
| C. | C的速度不变,A、B的速度变为v1和v2,且满足Mv0=Mv1+mv2 | |
| D. | A、C的速度都变为v1,B的速度变为v2,且满足(M+m0) v0=(M+m0) v1+mv2 |
 如图所示,将质量为m的小球用长为L的细线拴住,线的另一端固定在O点,将小球拉到与O等高的位置并使线刚好绷直,由静止开始释放小球,不计空气阻力.下列说法正确的是( )
如图所示,将质量为m的小球用长为L的细线拴住,线的另一端固定在O点,将小球拉到与O等高的位置并使线刚好绷直,由静止开始释放小球,不计空气阻力.下列说法正确的是( )| A. | 在落到最低点之前,小球的重力一直做正功,线的拉力不做功 | |
| B. | 小球在下落过程中,下落到最低点时速度达到最大 | |
| C. | 小球在下落过程中,机械能逐渐增大 | |
| D. | 小球在下落过程中机械能守恒 |
 如图所示,质量为m=5kg的金属块放在水平地面上,在与水平方向成θ=37°角斜向上的拉力F=20N作用下向右做匀速直线运动,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
如图所示,质量为m=5kg的金属块放在水平地面上,在与水平方向成θ=37°角斜向上的拉力F=20N作用下向右做匀速直线运动,(sin37°=0.6,cos37°=0.8,g=10m/s2)求: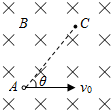 一质量为m,电量为+q的带电粒子在磁感强度为B的匀强磁场中,以初速度υ0垂直于磁场由A点开始运动,如图所示,经过时间t粒子通过C点,求连在AC与υ0间的夹角θ.
一质量为m,电量为+q的带电粒子在磁感强度为B的匀强磁场中,以初速度υ0垂直于磁场由A点开始运动,如图所示,经过时间t粒子通过C点,求连在AC与υ0间的夹角θ.