题目内容
(16分)某次燃放“爆竹”过程中,质量M=0.3kg(内含炸药的质量可以忽略不计)的“爆竹”从地面上以初速度v0 =30m/s竖直向上腾空而起。到达最高点时炸裂为沿水平方向相反飞行的两块,其中A块质量m=0.2kg,其炸裂瞬间的速度大小是另一块的一半。按环保和安全要求,两块都能落到以发射点为圆心、半径R=60m的圆周内。空气阻力不计,重力加速度g=10m/s2。求:
(1)“爆竹”能够到达的最大高度;
(2)A块的最大落地速度;
(3)整个过程中,“爆竹”释放化学能的最大值。
(1)H=45m (2)v= m/s (3)E=165J
m/s (3)E=165J
解析试题分析:设炮弹上升到达最高点的高度为H,由 (1分)
(1分)
代入数据得到H=45m (2分)
(2)题目要求两弹片不能落到圆外,临界条件是小质量片(B)恰好落在圆周上
设B刚炸裂时的速度为 ,运动的时间为t
,运动的时间为t
根据平抛运动规律,有 (1分)
(1分)
R=v1t (1分)
代入数据得:v1=20m/s (1分)
则A刚炸裂时的速度大小为 (1分)
(1分)
由机械能守恒知  (1分)
(1分)
代入数据得落地速度的最大值:v= m/s(1分)
m/s(1分)
(3)爆竹在空中刚炸裂后,A、B的总动能 (2分)
(2分)
代入数据得Ek=30J (1分)
爆竹竖直上抛时的机械能为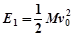 (2分)
(2分)
代入数据得:E1="135J" (1分)
根据能量关系知,最初动能和A、B动能,均来自化学能,故此次过程总共释放化学能为E=165J (1分)
考点:本题考查匀变速直线运动、机械能守恒定律和能量守恒定律。

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 ;滑块上表面光滑,其右端放置一质量m=0.2kg的小球。现给滑块一水平向右的瞬时冲量
;滑块上表面光滑,其右端放置一质量m=0.2kg的小球。现给滑块一水平向右的瞬时冲量 ,经过一段时间后小球落地。求小球落地时距滑块左端的水平距离。
,经过一段时间后小球落地。求小球落地时距滑块左端的水平距离。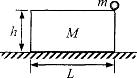

 倍。已知杆向上运动时,刚穿过PQ时的速度是刚穿过MN时速度的一半,杆从PQ上升的最大高度(未超过轨道上端)是磁场高度的n倍;杆向下运动时,一进入磁场立即做匀速直线运动。除定值电阻外不计其它一切电阻,已知重力加速度为g。求:
倍。已知杆向上运动时,刚穿过PQ时的速度是刚穿过MN时速度的一半,杆从PQ上升的最大高度(未超过轨道上端)是磁场高度的n倍;杆向下运动时,一进入磁场立即做匀速直线运动。除定值电阻外不计其它一切电阻,已知重力加速度为g。求:

