题目内容
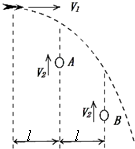
在某高度处以初速度v1水平抛出一个飞镖,在离抛出点水平距离l、2l处有A、B两个正以速度v2匀速上升的完全相同的小气球,先后被飞标刺破(认为飞标质量很大,刺破气球不会改变其平抛运动的轨迹).求:
(1)飞标刺破A气球时,飞标的速度大小;
(2)A、B两个小气球在未被刺破前的高度差.
(1)飞标刺破A气球时,飞标的速度大小;
(2)A、B两个小气球在未被刺破前的高度差.

(1)从抛出到刺破气球A,经过了时间 tA=
竖直方向速度 vy=gtA=
,
则飞镖速度 vA=
(2)AB两球被刺破位置的高度差 h1=3×
g
=
B球比A球多运动时间
,
B比A多上升 h2=v2
所以AB未被刺破前高度差为:H=h1+h2=
+
答:
(1)飞标刺破A气球时,飞标的速度大小为
;
(2)A、B两个小气球在未被刺破前的高度差为
+
.
| l |
| v1 |
竖直方向速度 vy=gtA=
| gl |
| v1 |
则飞镖速度 vA=
|
(2)AB两球被刺破位置的高度差 h1=3×
| 1 |
| 2 |
| t | 2A |
| 3gl2 | ||
2
|
B球比A球多运动时间
| l |
| v1 |
B比A多上升 h2=v2
| l |
| v1 |
所以AB未被刺破前高度差为:H=h1+h2=
| 3gl2 | ||
2
|
| v2l |
| v1 |
答:
(1)飞标刺破A气球时,飞标的速度大小为
|
(2)A、B两个小气球在未被刺破前的高度差为
| 3gl2 | ||
2
|
| v2l |
| v1 |

练习册系列答案
相关题目