题目内容
如图所示，平行金属板A和B间距离为d，现给A、B板加上如图所示的方波形电压，t=0时刻A板比B板的电势高，电压的正向值与反向值均为U0．现有由质量为m、电荷量为+q的粒子组成粒子束，从AB的中点O处以平行于金属板方向的速度v0=
沿OO’射入，所有粒子在金属板间的飞行时间均为T，不计重力影响．求：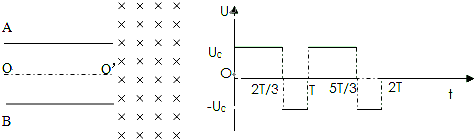
（1）不同时刻进入电场的粒子射出电场时的速度大小和方向
（2）平行金属板右侧为平行边界磁场，左右边界方向与OO’垂直，宽度为L，方向垂直纸面向里，所有粒子进入磁场后垂直右边界射出，问磁感应强度的大小．
| ||
| 3dm |
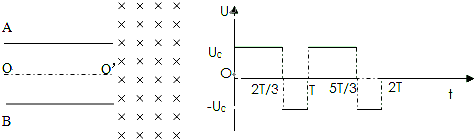
（1）不同时刻进入电场的粒子射出电场时的速度大小和方向
（2）平行金属板右侧为平行边界磁场，左右边界方向与OO’垂直，宽度为L，方向垂直纸面向里，所有粒子进入磁场后垂直右边界射出，问磁感应强度的大小．
分析：一种情况在0-
T之间，t0时刻进入电场的粒子运动情况相同，还有一种情况在
T-T之间进入电场的粒子运动情况相同，分别利用类平抛运动规律求其在射出电场时速度大小和方向；
所有粒子进入磁场后垂直右边界射出的临界情况为与右边界相切，根据几何知识确定半径，然后根据牛顿第二定律列方程求磁感应强度大小．
| 2 |
| 3 |
| 2 |
| 3 |
所有粒子进入磁场后垂直右边界射出的临界情况为与右边界相切，根据几何知识确定半径，然后根据牛顿第二定律列方程求磁感应强度大小．
解答：解：（1）设在0-
T之间，t0时刻进入电场，a=
vy=a（
T-t0）-a
+at0=
=
v=
=
tanθ=
=
θ=30°，方向斜向下；
设在
T-T之间进入电场，速度vy=
根据周期性，在任何时刻进入电场，射出电场时，v=
θ=300，
（2）由几何关系得，R=
=2L，qvB=m
B=
=
答：（1）不同时刻进入电场的粒子射出电场时的速度大小为
，方向与水平方向成30°角斜向下；
（2）平行金属板右侧为平行边界磁场，左右边界方向与OO′垂直，宽度为L，方向垂直纸面向里，所有粒子进入磁场后垂直右边界射出，磁感应强度的大小为
．
| 2 |
| 3 |
| qU0 |
| dm |
| 2 |
| 3 |
| T |
| 3 |
| aT |
| 3 |
| qU0T |
| 3dm |
v=
| v02+vy2 |
| 2qU0T |
| 3dm |
tanθ=
| vy |
| v0 |
| ||
| 3 |
设在
| 2 |
| 3 |
| qU0T |
| 3dm |
根据周期性，在任何时刻进入电场，射出电场时，v=
| 2qU0T |
| 3dm |
（2）由几何关系得，R=
| L |
| sin30° |
| v2 |
| R |
B=
| mv |
| qR |
| U0T |
| 3dL |
答：（1）不同时刻进入电场的粒子射出电场时的速度大小为
| 2qU0T |
| 3dm |
（2）平行金属板右侧为平行边界磁场，左右边界方向与OO′垂直，宽度为L，方向垂直纸面向里，所有粒子进入磁场后垂直右边界射出，磁感应强度的大小为
| U0T |
| 3dL |
点评：本题主要考查了带电粒子在混合场中运动的问题，要求同学们能正确分析粒子的受力情况，再通过受力情况分析粒子的运动情况，熟练掌握圆周运动及平抛运动的基本公式．
练习册系列答案
相关题目
如图所示，平行金属板长L，间距L，两板间存在向下的匀强电场E，一带电粒子（不计重力）沿两板中线以速度V0垂直射入电场，恰好从下板边缘P点射出平行金属板．若将匀强电场换成垂直纸面的匀强磁场，粒子仍然从同一点以同样的速度射入两板间，要粒子同样从P点射出，求：
（2011?吉安模拟）如图所示，平行金属板A、B带有等量异号电荷，电子和质子均以速率v分别从正（A板）、负（B板）两极板上的小孔沿垂直板面的方向射入板间，那么（ ）
如图所示，平行金属板与水平方向成θ角，板间距离为d，板间电压为U，一质量为m的带电微粒，以水平初速度v0从下板左端边缘进入板间，结果正好沿水平直线通过从上板右端上边缘处射出，求：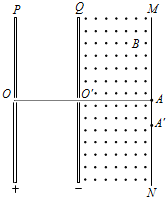
如图所示，平行金属板P、Q的中心分别有小孔O和O′，OO′连线与金属板垂直，两板间的电压为U．在Q板的右侧存在匀强磁场，磁场方向垂直纸面向外，磁感应强度为B．磁场右侧边界处的荧光屏MN与Q板间的距离为L，OO′连线的延长线与MN相交于A点．一质量为m、电荷量为+q的带电粒子，从小孔O处由静止开始运动，通过小孔O′后进入磁场，最终打在MN上的A′点．不计粒子重力．求：
磁流体发电是一项新兴技术，它可以把物体的内能直接转化为电能，如图所示，平行金属板A、B之间相距为d，板间的磁场按匀强磁场处理，磁感应强度为B，等离子体以速度v沿垂直于B的方向射入磁场，金属板A、B是边长为a的正方形，等离子体的电阻率为ρ，外接电阻R．求：