题目内容
8.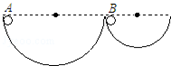 如图所示,两个半径不同而内壁光滑的半圆轨道固定于地面,一个小球先后从与球心在同一水平高度的A、B两点由静止开始自由下滑,通过轨道最低点时( )
如图所示,两个半径不同而内壁光滑的半圆轨道固定于地面,一个小球先后从与球心在同一水平高度的A、B两点由静止开始自由下滑,通过轨道最低点时( )| A. | 小球对两轨道的压力相同 | B. | 小球对两轨道的压力不同 | ||
| C. | 此时小球的向心加速度相等 | D. | 此时小球的向心加速度不相等 |
分析 小球从与球心在同一水平高度的A、B两点由静止开始自由下滑过程中,受到重力和支持力作用,但只有重力做功,机械能守恒,由机械能守恒定律可求出小球到最低点的速度,然后由向心加速度公式求向心加速度,由牛顿第二定律求出支持力,进而来比较向心加速度大小和压力大小.
解答 解:A、设半圆轨道的半径为r,小球到最低点的速度为v,由机械能守恒定律得:mgr=$\frac{1}{2}$mv2,在最低点,由牛顿第二定律得:FN-mg=m$\frac{{v}^{2}}{r}$,联立解得;FN=3mg,即压力为3mg,也与半径无关,所以小球对轨道的压力相同.故A正确,B错误.
C、设小球的向心加速度an=$\frac{{v}^{2}}{r}$,联立两式解得:an=2g,与半径无关,因此此时小球的向心加速度相等,故C正确,D错误;
故选:AC.
点评 明确机械能守恒的条件,知道小球下滑过程中,机械能守恒,根据机械能守恒定律、牛顿第二定律、向心力公式分别求出小球在最低点的压力和向心加速度,可以看出它们与圆轨道的半径无关.

练习册系列答案
相关题目
18.关于平均速度和瞬时速度的说法中正确的是( )
| A. | 平均速度就是初末时刻瞬时速度的平均值 | |
| B. | 平均速度等于零,则物体一定是静止的 | |
| C. | 平均速度可以精确描述物体的运动 | |
| D. | 瞬时速度的方向为轨迹某点的切线方向 |
19.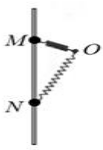 如图,小球套在光滑的竖直杆上,轻弹簧一端固定于O点,另一端与小球相连.现将小球从M点由静止释放,它在下降的过程中经过了N点.已知M、N两点处,弹簧对小球的弹力大小相等,且∠ONM<∠OMN<$\frac{π}{2}$.在小球从M点运动到N点的过程中,( )
如图,小球套在光滑的竖直杆上,轻弹簧一端固定于O点,另一端与小球相连.现将小球从M点由静止释放,它在下降的过程中经过了N点.已知M、N两点处,弹簧对小球的弹力大小相等,且∠ONM<∠OMN<$\frac{π}{2}$.在小球从M点运动到N点的过程中,( )
 如图,小球套在光滑的竖直杆上,轻弹簧一端固定于O点,另一端与小球相连.现将小球从M点由静止释放,它在下降的过程中经过了N点.已知M、N两点处,弹簧对小球的弹力大小相等,且∠ONM<∠OMN<$\frac{π}{2}$.在小球从M点运动到N点的过程中,( )
如图,小球套在光滑的竖直杆上,轻弹簧一端固定于O点,另一端与小球相连.现将小球从M点由静止释放,它在下降的过程中经过了N点.已知M、N两点处,弹簧对小球的弹力大小相等,且∠ONM<∠OMN<$\frac{π}{2}$.在小球从M点运动到N点的过程中,( )| A. | 弹力对小球先做正功后做负功 | |
| B. | 有两个时刻小球的加速度等于重力加速度 | |
| C. | 弹簧长度最短时,弹力对小球做功的功率不为零 | |
| D. | 小球到达N点时的动能等于其在M、N两点的重力势能差 |
18.以下的计时数据指时间的是( )
| A. | 某人用15s跑完100m | |
| B. | 早上6点起床 | |
| C. | 中央电视台新闻联播节目19时开播 | |
| D. | 天津开往德州的625次硬座普快列车于13h35min从天津西站发车 |
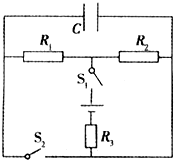 如图所示电路中,R1=3Ω,R2=6Ω,R3=1.5Ω,C=20 μF;已知电源电动势E=4V,内阻r=0.5Ω.求:
如图所示电路中,R1=3Ω,R2=6Ω,R3=1.5Ω,C=20 μF;已知电源电动势E=4V,内阻r=0.5Ω.求: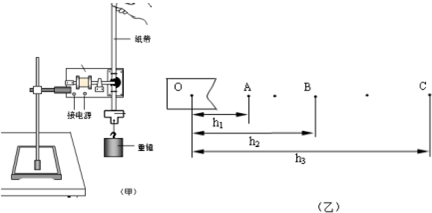
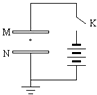 如图所示,在平行板电容器正中有一个带电微粒.K闭合时,该微粒恰好能保持静止.充电后将K断开;稍微向左移动上极板M,该带电微粒向上运动.(填”上”或”下”)
如图所示,在平行板电容器正中有一个带电微粒.K闭合时,该微粒恰好能保持静止.充电后将K断开;稍微向左移动上极板M,该带电微粒向上运动.(填”上”或”下”)