题目内容
18.太阳系中某行星运行的轨道半径为R0,周期为T0,天文学家在长期观测中发现,其实际运行的轨道总是存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离(行星仍然近似做匀速圆周运动).天文学家认为形成这种现象的原因可能是该行星外侧还存在着一颗未知行星.假设两行星的运行轨道在同一平面内,且绕行方向相同,则这颗未知行星运行轨道的半径R和周期T是(认为未知行星近似做匀速圆周运动)( )| A. | T=$\frac{{t}_{0}^{2}}{{t}_{0}-{T}_{0}}$ | B. | $R={R_0}\root{3}{{{{(\frac{t_0}{{{t_0}-{T_0}}})}^2}}}$ | ||
| C. | T=$\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$T0 | D. | R=R0$\root{3}{(\frac{{t}_{0}-{T}_{0}}{{t}_{0}})^{2}}$ |
分析 当两行星相距最近时,未知行星对该行星的影响最大,且每隔t0时间相距最近,可知在t0时间内该卫星比未知卫星多运行1圈,结合该关系求出B的周期.由开普勒第三定律求出未知行星的轨道半径
解答 解:AC、行星发生最大偏离时,两行星与恒星在同一直线上且位于恒星同一侧.设未知行星运行周期为T,轨道半径为R,则有:($\frac{2π}{{T}_{0}}$-$\frac{2π}{T}$)t0=2π
解得未知行星的运行周期为:T=$\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$T0,故C正确,A错误.
BD、由开普勒第三定律有:$\frac{{R}_{0}^{3}}{{T}_{0}^{2}}$=$\frac{{T}_{0}^{2}}{{T}^{2}}$,解得:R=R0$\root{3}{(\frac{{t}_{0}}{{t}_{0}-{T}_{0}})^{2}}$,则B正确,D错误
故选:BC
点评 本题考查了万有引力定律的运用,掌握万有引力提供向心力这一理论,并能灵活运用,知道A、B相距最近时,B对A的影响最大,且每隔t0时间相距最近.

练习册系列答案
相关题目
8.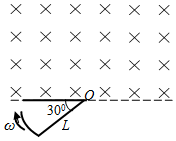 如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )
如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )
 如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )
如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )| A. | $\frac{B{L}^{2}ω}{72R}$ | B. | $\frac{\sqrt{6}B{L}^{2}ω}{12R}$ | C. | $\frac{\sqrt{2}B{L}^{2}ω}{4R}$ | D. | $\frac{\sqrt{3}B{L}^{2}ω}{2R}$ |
13. 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )
 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A. | 由n=4能级跃迁到n=1能级产生的光子波长最长 | |
| B. | 由n=2能级跃迁到n=1能级产生的光子频率最小 | |
| C. | 这些氢原子总共可辐射出3种不同频率的光 | |
| D. | 用n=2能级跃迁到n=1能级辐射出的光照射逸出功为6.34 eV的金属铂能发生光电效应 |
3.关于理想气体的内能,下列说法正确的是( )
| A. | 气体在膨胀时,内能可能不变 | |
| B. | 质量和温度都相同的气体,内能一定相同 | |
| C. | 一定质量的某种理想气体在等压压缩过程中,内能一定减少 | |
| D. | 气体温度不变,整体运动速度越大,其内能越大 |
7. 如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
 如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )| A. | m能到达圆弧轨道右侧的最高位置与初始位置等高 | |
| B. | m能到达圆弧轨道右侧的最高位置比初始位置低,不会滑出圆弧轨道 | |
| C. | m能到达圆弧轨道右侧的最高位置比初始位置高,将滑出圆弧轨道 | |
| D. | m到达圆弧轨道右侧最高位置时,M将会向左移动一段位移 |
11.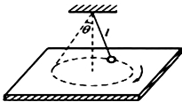 如图所示,长为l的绳子下端连着质量为m的小球,上端悬于天花板上,当绳子拉直时,绳子与竖直方向的夹角为60°,此时,小球静止于光滑水平桌面上,重力加速度为g.则( )
如图所示,长为l的绳子下端连着质量为m的小球,上端悬于天花板上,当绳子拉直时,绳子与竖直方向的夹角为60°,此时,小球静止于光滑水平桌面上,重力加速度为g.则( )
 如图所示,长为l的绳子下端连着质量为m的小球,上端悬于天花板上,当绳子拉直时,绳子与竖直方向的夹角为60°,此时,小球静止于光滑水平桌面上,重力加速度为g.则( )
如图所示,长为l的绳子下端连着质量为m的小球,上端悬于天花板上,当绳子拉直时,绳子与竖直方向的夹角为60°,此时,小球静止于光滑水平桌面上,重力加速度为g.则( )| A. | 当小球以角速度ω=$\sqrt{\frac{g}{l}}$做圆锥摆运动时,绳子的张力大小等于重力大小 | |
| B. | 当小球以角速度ω=$\sqrt{\frac{g}{l}}$做圆锥摆运动时,桌面对小球的支持力大小等于重力大小 | |
| C. | 当小球以角速度ω=2$\sqrt{\frac{g}{l}}$做圆锥摆运动时,绳子的张力大小等于重力大小的3倍 | |
| D. | 当小球以角速度ω=$\sqrt{\frac{2g}{l}}$做圆锥摆运动时,桌面对小球恰好没有支持力的作用 |
 如图所示,内壁光滑、导热良好的汽缸中封闭了一定质量的理想气体,活塞到缸底的距离h=0.5m.已知活塞质量m=2kg,横截面积S=1×10-3m2,环境温度t=0℃且保持不变,外界大气压强p0=1×105Pa,阿伏加德罗常数NA=6×1023mol-1,标准状态下气体的摩尔体积Vmol=22.4L/mol,g=10m/s2.现将汽缸缓慢地转至开口水平,求:
如图所示,内壁光滑、导热良好的汽缸中封闭了一定质量的理想气体,活塞到缸底的距离h=0.5m.已知活塞质量m=2kg,横截面积S=1×10-3m2,环境温度t=0℃且保持不变,外界大气压强p0=1×105Pa,阿伏加德罗常数NA=6×1023mol-1,标准状态下气体的摩尔体积Vmol=22.4L/mol,g=10m/s2.现将汽缸缓慢地转至开口水平,求: 如图所示,半径为R的半圆柱形玻璃砖某一截面的圆心为O点.有两条光线垂直于水平柱面射入玻璃砖中,其中一条光线通过圆心O,另一条光线通过A点,且OA=2R.这两条光线射出玻璃砖后相交于一点,该点到O点的距离为R,求玻璃的折射率.
如图所示,半径为R的半圆柱形玻璃砖某一截面的圆心为O点.有两条光线垂直于水平柱面射入玻璃砖中,其中一条光线通过圆心O,另一条光线通过A点,且OA=2R.这两条光线射出玻璃砖后相交于一点,该点到O点的距离为R,求玻璃的折射率.