题目内容
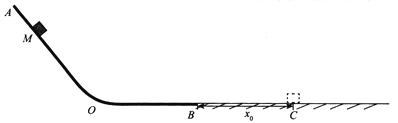
【题目】如图所示,某拱桥的拱高为h,弧长为L,一质量为m的汽车以不变的速率由P运动到Q,已知汽车与桥面的动摩擦因数为μ,则在此过程中()
![]()
A. 汽车的牵引力保持不变
B. 重力做功为2mgh
C. 摩擦力做功为-μmgL
D. 牵引力做功与摩擦力做功的代数和为零
【答案】D
【解析】
汽车受重力、支持力、牵引力和摩擦力,汽车做匀速圆周运动,切向分量平衡,根据平衡条件,有:F=mgsinθ+μmgcosθ (θ为坡角),由于坡角θ先减小后增加,故牵引力F是变化的,故A错误;初末位置高度相同,故重力做功为零,故B错误;对汽车受力分析,汽车受重力、支持力、牵引力和摩擦力;取一小段位移△L,简化为斜面,克服摩擦力做功为:△Wf=μmgcosθ△L,故全程摩擦力做功为:Wf=∑△Wf=∑μmgcosθ△L=μmgPQ<μmgL,故C错误;整个过程受重力、支持力、牵引力和摩擦力,重力和支持力不做功,根据动能定理,有:W=△Ek=0,即牵引力做功与摩擦力做功的代数和为零,故D正确。

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案【题目】(6分)某物理小组的同学设计了一个粗制玩具小车通过凹形桥最低点时的速度的实验。所用器材有:玩具小车、压力式托盘秤、凹形桥模拟器(圆弧部分的半径为R=0.20m)。
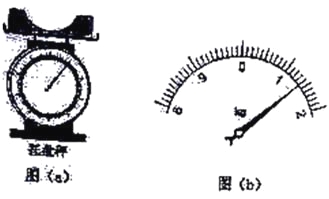
完成下列填空:
(1)将凹形桥模拟器静置于托盘秤上,如图(a)所示,托盘秤的示数为1.00kg;
(2)将玩具小车静置于凹形桥模拟器最低点时,托盘秤的示数如图(b)所示,该示数为_____kg;
(3)将小车从凹形桥模拟器某一位置释放,小车经过最低点后滑向另一侧,此过程中托盘秤的最大示数为m;多次从同一位置释放小车,记录各次的m值如下表所示:
序号 | 1 | 2 | 3 | 4 | 5 |
m(kg) | 1.80 | 1.75 | 1.85 | 1.75 | 1.90 |
(4)根据以上数据,可求出小车经过凹形桥最低点时对桥的压力为_____N;小车通过最低点时的速度大小为_______m/s。(重力加速度大小取9.80m/s2 ,计算结果保留2位有效数字)