题目内容
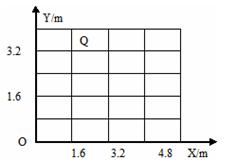
 如图所示在竖直平面内建立直角坐标系XOY,OY表示竖直向上的方向.已知该平面内存在沿OX轴负方向的区域足够大的匀强电场,现有一个带电量为2.5×10-7C、质量为10-5Kg的小球从坐标原点O沿Y轴正方向以某一初速度竖直向上抛出,它到达的最高点位置为图中的Q点,其坐标为(1.6,3.2),不计空气阻力,g取10m/s2.求:
如图所示在竖直平面内建立直角坐标系XOY,OY表示竖直向上的方向.已知该平面内存在沿OX轴负方向的区域足够大的匀强电场,现有一个带电量为2.5×10-7C、质量为10-5Kg的小球从坐标原点O沿Y轴正方向以某一初速度竖直向上抛出,它到达的最高点位置为图中的Q点,其坐标为(1.6,3.2),不计空气阻力,g取10m/s2.求:(1)指出小球带何种电荷;
(2)小球的初速度和匀强电场的场强大小;
(3)小球从O点抛出到落回X轴的过程中电势能的改变量.
分析:本题的关键是将小球运动看成是竖直方向的竖直上抛运动和水平方向的初速度为零的匀加速直线运动合成的,然后根据竖直上抛运动规律求出到最高点的时间,从而再根据牛顿运动定律求出水平方向的场强,然后求出电场力做的功即可.
解答:解:(1)带电小球所到的最高点Q在O点的右上方,说明小球有水平向右的分运动和竖直向上的分运动就竖直方向而言,初速度是竖直向上的而重力是竖直向下的,重力使竖直向上的初速度逐渐减小,而不会产生水平向右的运动.小球只受重力和电场力,只有电场力水平向右才会使小球有向右的分运动.由此可以判断电场力是水平向右的,又因为电场水平向左,所以小球带负电.
故小球带负电.
(2)对小球的两个分运动,竖直方向:小球有竖直向上的初速度V0,受重力,所以小球做竖直上抛运动.Q点是最高点意味着Q点的竖直分速度为0.由竖直上抛运动得:v0=
=8m/s,上式时间t=
=0.8s
水平方向:水平初速度为0,水平位移有x=
,解得a=5m/s2
小球在水平方向的加速度a=
=
得E=200N/C
故小球的初速度为8m/s,匀强电场的场强大小为200N/C.
(3)小球从O点落回到X轴时,由于对称性,水平位移为
=
a(2t
,代入数据得
=6.4m,
电场力做的功为W=qE
=3.2
J,所以电势能减少了3.2×10-4J(或电势能改变量为-3.2
J).
故小球从O点抛出到落回X轴的过程中电势能减少了3.2
J.
故小球带负电.
(2)对小球的两个分运动,竖直方向:小球有竖直向上的初速度V0,受重力,所以小球做竖直上抛运动.Q点是最高点意味着Q点的竖直分速度为0.由竖直上抛运动得:v0=
| 2gh |
| v0 |
| g |
水平方向:水平初速度为0,水平位移有x=
| 1 |
| 2 |
| at | 2 |
小球在水平方向的加速度a=
| F |
| q |
| qE |
| m |
故小球的初速度为8m/s,匀强电场的场强大小为200N/C.
(3)小球从O点落回到X轴时,由于对称性,水平位移为
| x | ′ |
| 1 |
| 2 |
| ) | 2 |
| x | ′ |
电场力做的功为W=qE
| x | ′ |
| ×10 | -4 |
| ×10 | -4 |
故小球从O点抛出到落回X轴的过程中电势能减少了3.2
| ×10 | -4 |
点评:遇到匀变速曲线运动问题,可以通过受力分析,将曲线运动分解为互相垂直的匀变速直线运动,然后根据运动的等时性和相应规律列式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

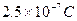 、质量为
、质量为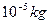 的小球从坐标
的小球从坐标 原点O沿Y轴正方向以某一初速度竖直向上抛出,它到达的最高点位置为图中的Q点,其坐标为(1.6,3.2),不计空气阻力,g取10m/s2。
原点O沿Y轴正方向以某一初速度竖直向上抛出,它到达的最高点位置为图中的Q点,其坐标为(1.6,3.2),不计空气阻力,g取10m/s2。