题目内容
13.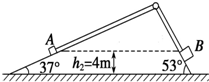 如图所示,一个三角形光滑斜面在水平地面上,底角分别为37°、53°,A、B两小物块质量分别为mA=2kg、mB=3kg,用轻绳连接,通过小轻质滑轮跨放在左右两斜面上,轻绳伸直时,两物块离地高度h2=4m,在滑轮处压住细绳,三角形斜面始终静止.(g=10m/s2,sin 37°=0.6,sin 53°=0.8 )
如图所示,一个三角形光滑斜面在水平地面上,底角分别为37°、53°,A、B两小物块质量分别为mA=2kg、mB=3kg,用轻绳连接,通过小轻质滑轮跨放在左右两斜面上,轻绳伸直时,两物块离地高度h2=4m,在滑轮处压住细绳,三角形斜面始终静止.(g=10m/s2,sin 37°=0.6,sin 53°=0.8 ) (1)若在压绳处突然剪断绳,求A、B下滑过程中加速度之比;
(2)若松开绳,求B滑到底端时的速度大小;
(3)若松开绳,求地面给斜面的摩擦力.
分析 (1)分别对AB受力分析,利用牛顿第二定律求解即可.
(2)对整体利用能量守恒定律求解即可.
(3)松开绳子,设绳子上的拉力是T,分别对A和B进行受力分析,求出拉力T,然后对整体进行受力分析即可求出.
解答 解:(1)对A分析有 mAgsin 37°=maA
对B分析有 mBgsin 53°=maB
解得 $\frac{{a}_{A}}{{a}_{B}}=\frac{gsin37°}{gsin53°}$=0.75,
(2)对AB整体有能量守恒定律可知:
${m}_{B}g{h}_{2}-{m}_{A}g{h}_{A}=\frac{1}{2}({m}_{A}+{m}_{B}){v}^{2}$
由几何关系得:h2=hB=4m,hA=$\frac{{h}_{2}}{sin53°}$•sin37°=3m
代入数据得:3×10×4-2×10×3=$\frac{1}{2}$(2+3)v2
解得:v=$2\sqrt{6}$m/s
(3)设绳子的拉力为T,对A分析有 T-mAgsin 37°=mAa
对B分析有 mBgsin 53°-T=mBa
代入数据整理得:a=2.4m/s2
对整体分析得:f=mAa•cos37°+mBcos53°
代入数据得:f=8.16N
答:(1)A、B下滑过程中加速度之比为0.75,
(2)B滑到底端时的速度大小为$2\sqrt{6}$m/s;
(3)若松开绳,地面给斜面的摩擦力是8.16N.
点评 本题考查牛顿第二定律和能量守恒定律的应用,第一问难度不大,第二问中整体利用能量守恒是关键,特别是位移及高度变化之间关系.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
3.将力F分解成F1和F2,若已知F1的大小和F2与F的夹角(θ为锐角),则下列说法中错误的是( )
| A. | 当F1>Fsin θ时,有两解 | B. | 当F1=Fsin θ时,一解 | ||
| C. | 当Fsin θ<F1<F时,有三解 | D. | 当F1<Fsin θ时,无解 |
4.一列简谐横波在某时刻的波形图如图所示,波速为20m/s,以下说法正确的是( )

| A. | 这列波沿x轴正方向传播 | |
| B. | 质点a在图示时刻的振动方向沿y轴正方向 | |
| C. | 质点a在图示时刻的加速度方向沿y轴正方向 | |
| D. | 从图示时刻开始,质点a经0.1s通过的路程为0.4m |
1. 如图所示,A、B两物块的质量均为m,把它们靠在一起从一个坡面光滑质量为M的斜面C顶端由静止开始下滑.已知斜面的倾角为θ,斜面始终保持静止.则在此过程中,以下说法正确的是( )
如图所示,A、B两物块的质量均为m,把它们靠在一起从一个坡面光滑质量为M的斜面C顶端由静止开始下滑.已知斜面的倾角为θ,斜面始终保持静止.则在此过程中,以下说法正确的是( )
 如图所示,A、B两物块的质量均为m,把它们靠在一起从一个坡面光滑质量为M的斜面C顶端由静止开始下滑.已知斜面的倾角为θ,斜面始终保持静止.则在此过程中,以下说法正确的是( )
如图所示,A、B两物块的质量均为m,把它们靠在一起从一个坡面光滑质量为M的斜面C顶端由静止开始下滑.已知斜面的倾角为θ,斜面始终保持静止.则在此过程中,以下说法正确的是( )| A. | A、B两物体间的作用力为2mgsinθ | B. | A、B两物体间作用力为0 | ||
| C. | 斜面对地面的压力为Mg+2mg | D. | 地面对斜面的摩擦力方向向左 |
8. 如图所示,质量不变的物块放置在足够长的水平面上,物块在水平拉力作用下由静止开始运动,运动中所受阻力与物块速度的大小成正比,现用两种方式使物块运动:一是保持拉力的大小恒定,当物块速度为v时加速度为a1,最终物块以速度2v做匀速直线运动;二是保持拉力的功率恒定,当物块速度为v时加速度为a2,最终物块也以速度2v做匀速直线运动,则( )
如图所示,质量不变的物块放置在足够长的水平面上,物块在水平拉力作用下由静止开始运动,运动中所受阻力与物块速度的大小成正比,现用两种方式使物块运动:一是保持拉力的大小恒定,当物块速度为v时加速度为a1,最终物块以速度2v做匀速直线运动;二是保持拉力的功率恒定,当物块速度为v时加速度为a2,最终物块也以速度2v做匀速直线运动,则( )
 如图所示,质量不变的物块放置在足够长的水平面上,物块在水平拉力作用下由静止开始运动,运动中所受阻力与物块速度的大小成正比,现用两种方式使物块运动:一是保持拉力的大小恒定,当物块速度为v时加速度为a1,最终物块以速度2v做匀速直线运动;二是保持拉力的功率恒定,当物块速度为v时加速度为a2,最终物块也以速度2v做匀速直线运动,则( )
如图所示,质量不变的物块放置在足够长的水平面上,物块在水平拉力作用下由静止开始运动,运动中所受阻力与物块速度的大小成正比,现用两种方式使物块运动:一是保持拉力的大小恒定,当物块速度为v时加速度为a1,最终物块以速度2v做匀速直线运动;二是保持拉力的功率恒定,当物块速度为v时加速度为a2,最终物块也以速度2v做匀速直线运动,则( )| A. | a2=a1 | B. | a2=2a1 | C. | a2=3a1 | D. | a2=4a1 |
18.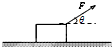 如图所示,一物体放在粗糙水平地面上,对物体施加一个倾角为θ的斜向上方的力F,当这个力从零开始逐渐增大时,此过程中,物体将由静止变运动,但不会脱离地面.物体在此过程中受到的摩擦力的变化情况是( )
如图所示,一物体放在粗糙水平地面上,对物体施加一个倾角为θ的斜向上方的力F,当这个力从零开始逐渐增大时,此过程中,物体将由静止变运动,但不会脱离地面.物体在此过程中受到的摩擦力的变化情况是( )
 如图所示,一物体放在粗糙水平地面上,对物体施加一个倾角为θ的斜向上方的力F,当这个力从零开始逐渐增大时,此过程中,物体将由静止变运动,但不会脱离地面.物体在此过程中受到的摩擦力的变化情况是( )
如图所示,一物体放在粗糙水平地面上,对物体施加一个倾角为θ的斜向上方的力F,当这个力从零开始逐渐增大时,此过程中,物体将由静止变运动,但不会脱离地面.物体在此过程中受到的摩擦力的变化情况是( )| A. | 逐渐增大 | B. | 逐渐减小 | ||
| C. | 先逐渐增大,后又减小 | D. | 先逐渐减小,后又增大 |
3.关于重力的说法,正确的是( )
| A. | 同一地点物体所受重力的大小仅与物体质量有关,与物体是否运动及怎样运动无关 | |
| B. | 物体本身就有重力,所以重力没有施力物体 | |
| C. | 物体受到的重力,就作用在重心上 | |
| D. | 具有规则几何形状的物体的重心,不一定就在其几何中心 |

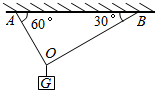 如图,A的最大拉力是100N,B的最大拉力是80N,问逐渐增加所挂物体的质量,两条绳谁先断?这时所挂的重物最大质量是多少?
如图,A的最大拉力是100N,B的最大拉力是80N,问逐渐增加所挂物体的质量,两条绳谁先断?这时所挂的重物最大质量是多少?