题目内容
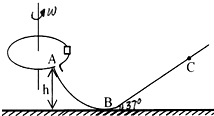 如图所示,一半径R=0.2m的水平圆盘绕过圆心的竖直轴转动,圆盘边缘有一质量m=1.0kg的小滑块.当圆盘转动的角速度达到某一数值时,滑块从圆盘边缘滑落,经光滑的过渡圆管(图中圆管未画出)进入轨道ABC.已知AB段为光滑的弧形轨道,A点离B点所在水平面的高度h=1.2m;BC斜面与AB轨道对接且倾角为37°,滑块与圆盘及BC斜面间的动摩擦因数均为μ=0.5,滑块在运动过程中始终未脱离轨道,不计在过渡圆管处和B点的机械能损失,设最大静摩擦力等于滑动摩擦力,取g=10m/s2,sin37°=0.6,cos37°=0.8
如图所示,一半径R=0.2m的水平圆盘绕过圆心的竖直轴转动,圆盘边缘有一质量m=1.0kg的小滑块.当圆盘转动的角速度达到某一数值时,滑块从圆盘边缘滑落,经光滑的过渡圆管(图中圆管未画出)进入轨道ABC.已知AB段为光滑的弧形轨道,A点离B点所在水平面的高度h=1.2m;BC斜面与AB轨道对接且倾角为37°,滑块与圆盘及BC斜面间的动摩擦因数均为μ=0.5,滑块在运动过程中始终未脱离轨道,不计在过渡圆管处和B点的机械能损失,设最大静摩擦力等于滑动摩擦力,取g=10m/s2,sin37°=0.6,cos37°=0.8(1)当圆盘的角速度多大时,滑块从圆盘上滑落?
(2)求滑块到达B点时的机械能(取地面为零势能参考面).
(3)从滑块到达B点时起,经0.6s正好通过C点,求BC之间的距离.
分析:(1)滑块做匀速圆周运动,指向圆心的静摩擦力力提供向心力,静摩擦力随着外力的增大而增大,当滑块即将从圆盘上滑落时,静摩擦力达到最大值,根据最大静摩擦力等于向心力列式求解,可以求出滑块即将滑落的临界角速度;
(2)先求出A点的速度,再根据机械能的表达式求解出B点的速度,进而求出在B点时的机械能;
(3)对滑块受力分析,分别求出向上滑行和向下滑行的加速度,然后根据运动学公式求解出BC间的距离.
(2)先求出A点的速度,再根据机械能的表达式求解出B点的速度,进而求出在B点时的机械能;
(3)对滑块受力分析,分别求出向上滑行和向下滑行的加速度,然后根据运动学公式求解出BC间的距离.
解答:解:(1)滑块在圆盘上做圆周运动时,静摩擦力充当向心力,根据牛顿第二定律,可得:
μmg=mω2R
代入数据解得:ω=5rad/s
(2)滑块在A点时的速度:VA=ωR=1m/s
滑块在从A到B的运动过程中机械能守恒:mgh+
mvA2=
mvB2
解得:
vB=5m/s
在B点时的机械能EB=
mvB2=12.5J
(3)滑块沿BC段向上运动时的加速度大小:a1=g(sin37°+μcos37°)=10m/s2
滑块沿BC段向上运动的时间:t1=
=0.5s 小于题中所给时间,滑块会返回一段时间
向上运动的位移:S1=
=1.25m
返回时的加速度大小:a2=g(sin37°-μcos37°)=2m/s2
S2=
a2(t-t1)2=0.01m
BC间的距离:sBC=S1-S2=1.24m
答:(1)当圆盘的角速度为5rad/s时,滑块从圆盘上滑落;
(2)滑块到达B点时的机械能为12.5J(取地面为零势能参考面).
(3)从滑块到达B点时起,经0.6s正好通过C点,BC之间的距离为1.24m.
μmg=mω2R
代入数据解得:ω=5rad/s
(2)滑块在A点时的速度:VA=ωR=1m/s
滑块在从A到B的运动过程中机械能守恒:mgh+
| 1 |
| 2 |
| 1 |
| 2 |
解得:
vB=5m/s
在B点时的机械能EB=
| 1 |
| 2 |
(3)滑块沿BC段向上运动时的加速度大小:a1=g(sin37°+μcos37°)=10m/s2
滑块沿BC段向上运动的时间:t1=
| vB |
| a1 |
向上运动的位移:S1=
| vB2 |
| 2a1 |
返回时的加速度大小:a2=g(sin37°-μcos37°)=2m/s2
S2=
| 1 |
| 2 |
BC间的距离:sBC=S1-S2=1.24m
答:(1)当圆盘的角速度为5rad/s时,滑块从圆盘上滑落;
(2)滑块到达B点时的机械能为12.5J(取地面为零势能参考面).
(3)从滑块到达B点时起,经0.6s正好通过C点,BC之间的距离为1.24m.
点评:本题关键把物体的各个运动过程的受力情况和运动情况分析清楚,然后结合动能定理、牛顿第二定律和运动学公式求解.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 (2013?德州一模)如图所示,一半径R=1m的圆盘水平放置,在其边缘 E点固定一小桶(可视为质点).在圆盘直径 DE 的正上方平行放置一水平滑道 BC,滑道右端 C点 与圆盘圆心O在同一竖直线上,且竖直高度 h=1.25m.AB为一竖直面内的光滑四分之一圆弧轨道,半径r=0.45m,且与水平滑道相切与B点.一质量m=0.2kg的滑块(可视为质点)从A点由静止释放,当滑块经过B点时,圆盘从图示位置以一定的角速度ω绕通过圆心的竖直轴匀速转动,最终物块由C 点水平抛出,恰好落入圆盘边缘的小桶内.已知滑块与滑道 BC间的摩擦因数μ=0.2.(取g=10m/s2)求
(2013?德州一模)如图所示,一半径R=1m的圆盘水平放置,在其边缘 E点固定一小桶(可视为质点).在圆盘直径 DE 的正上方平行放置一水平滑道 BC,滑道右端 C点 与圆盘圆心O在同一竖直线上,且竖直高度 h=1.25m.AB为一竖直面内的光滑四分之一圆弧轨道,半径r=0.45m,且与水平滑道相切与B点.一质量m=0.2kg的滑块(可视为质点)从A点由静止释放,当滑块经过B点时,圆盘从图示位置以一定的角速度ω绕通过圆心的竖直轴匀速转动,最终物块由C 点水平抛出,恰好落入圆盘边缘的小桶内.已知滑块与滑道 BC间的摩擦因数μ=0.2.(取g=10m/s2)求 如图所示,一半径R=0.2m的水平圆盘绕过圆心的竖直轴转动,圆盘边缘有一质量m=1.0kg的小滑块.当圆盘转动的角速度逐渐增大到某一数值时,滑块刚好从圆盘边缘处滑落,进入轨道ABC.已知AB段为光滑的圆弧形轨道,轨道半径r=2.5m,B点是圆弧形轨道与水平地面的相切点,A点与B点的高度差h=1.2m;倾斜轨道BC与圆轨道AB对接且倾角为37°,滑块与圆盘及BC轨道间的动摩擦因数均为μ=0.5,滑块在运动过程中始终未脱离轨道,不计滑块在A点和B点处的机械能损失,设最大静摩擦力等于滑动摩擦力,取g=10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,一半径R=0.2m的水平圆盘绕过圆心的竖直轴转动,圆盘边缘有一质量m=1.0kg的小滑块.当圆盘转动的角速度逐渐增大到某一数值时,滑块刚好从圆盘边缘处滑落,进入轨道ABC.已知AB段为光滑的圆弧形轨道,轨道半径r=2.5m,B点是圆弧形轨道与水平地面的相切点,A点与B点的高度差h=1.2m;倾斜轨道BC与圆轨道AB对接且倾角为37°,滑块与圆盘及BC轨道间的动摩擦因数均为μ=0.5,滑块在运动过程中始终未脱离轨道,不计滑块在A点和B点处的机械能损失,设最大静摩擦力等于滑动摩擦力,取g=10m/s2,sin37°=0.6,cos37°=0.8.
