题目内容
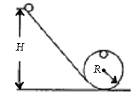
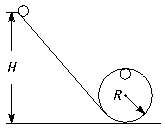
 有一质量为m的小球沿如下图所示的轨道下滑(倾斜部分与圆形部分平滑连接),小球离地面高度为H,倾斜部分粗糙,圆形轨道部分光滑,半径为R,小球恰好能通过最高点.求:
有一质量为m的小球沿如下图所示的轨道下滑(倾斜部分与圆形部分平滑连接),小球离地面高度为H,倾斜部分粗糙,圆形轨道部分光滑,半径为R,小球恰好能通过最高点.求:(1)摩擦阻力做的功.
(2)在轨道最低点小球对轨道的压力.
分析:(1)小球恰好能通过圆弧轨道最高点,说明此时恰好是物体的重力作为向心力,由向心力的公式可以求得在最高点的速度大小,再根据动能定理求解摩擦阻力做的功.
(2)先由机械能守恒定律求出小球经过最低点时的速度.在最低点时,对物体受力分析,重力和支持力的合力作为向心力,由向心力的公式可以求得小球受得支持力的大小,再由牛顿第三定律可以知道对轨道压力的大小.
(2)先由机械能守恒定律求出小球经过最低点时的速度.在最低点时,对物体受力分析,重力和支持力的合力作为向心力,由向心力的公式可以求得小球受得支持力的大小,再由牛顿第三定律可以知道对轨道压力的大小.
解答:解:(1)小球恰好能通过最高点在最高点,由重力提供向心力,则有:mg=m
,①
对于整个过程,由动能定理得:mg(H-2R)+Wf=
m
③
联立两式解得,Wf=
mgR-mg(H-2R)
(2)从最低点到最高点的过程,由机械能守恒定律得:
mg?2R+
m
=
m
在最低点,由牛顿第二定律得:N-mg=m
解得N=6mg
根据牛顿第三定律得:在轨道最低点小球对轨道的压力大小N′=N=6mg,方向竖直向下.
答:
(1)摩擦阻力做的功为
mgR-mg(H-2R).
(2)在轨道最低点小球对轨道的压力为6mgR,方向竖直向下.
| ||
| R |
对于整个过程,由动能定理得:mg(H-2R)+Wf=
| 1 |
| 2 |
| v | 2 高 |
联立两式解得,Wf=
| 1 |
| 2 |
(2)从最低点到最高点的过程,由机械能守恒定律得:
mg?2R+
| 1 |
| 2 |
| v | 2 高 |
| 1 |
| 2 |
| v | 2 低 |
在最低点,由牛顿第二定律得:N-mg=m
| ||
| R |
解得N=6mg
根据牛顿第三定律得:在轨道最低点小球对轨道的压力大小N′=N=6mg,方向竖直向下.
答:
(1)摩擦阻力做的功为
| 1 |
| 2 |
(2)在轨道最低点小球对轨道的压力为6mgR,方向竖直向下.
点评:本题的突破口是小球恰好能通过最高点,关键抓住重力等于向心力求出最高点的速度.

练习册系列答案
相关题目