题目内容
某人用力将一质量为m的物体从离地面高为h的地方竖直上抛,上升的最大高度为H(相对于抛出点),设抛出时初速度为v,落地时速度为vt,那么此人在抛出物体过程中对物体所做功为( )A.mgH
B.mgh
C.
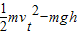
D.
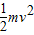
【答案】分析:根据已知量,对不同过程应用动能定理进行分析,即可得出人对物体所做的功.
解答:解:在人推于的过程中,由动能定理可得:
W= mv2; 故D正确;
mv2; 故D正确;
对全过程分析可知:
在球运动的过程中,球受人的抛出力做功,重力做功;且已知初动能和末动能,由动能定理可得:
W+mgh= mvt2-0:
mvt2-0:
解得人对球所做的功:W=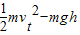 ;故C正确;
;故C正确;
对于从开始抛到最高点由动能定理可得:
W-mgH=0
故W=mgH,故A正确;
故选ACD.
点评:本题考查动能定理的应用,要求学生应正确理解题目中各量的意义,分别对不同的过程列式得出正确的结论.
解答:解:在人推于的过程中,由动能定理可得:
W=
 mv2; 故D正确;
mv2; 故D正确;对全过程分析可知:
在球运动的过程中,球受人的抛出力做功,重力做功;且已知初动能和末动能,由动能定理可得:
W+mgh=
 mvt2-0:
mvt2-0:解得人对球所做的功:W=
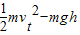 ;故C正确;
;故C正确;对于从开始抛到最高点由动能定理可得:
W-mgH=0
故W=mgH,故A正确;
故选ACD.
点评:本题考查动能定理的应用,要求学生应正确理解题目中各量的意义,分别对不同的过程列式得出正确的结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
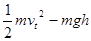 D.
D.