题目内容
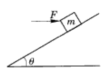
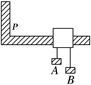
如图所示，质量之比为1:2的两木块A和B叠放在光滑水平面上，它们之间的最大静摩擦力为f，木块B与劲度系数为k的轻质弹簧连，弹簧的另一端固定在墙上。为使A和B在振动过程中不发生相对滑动，则它们的振幅不能大于 。
3f/k
试题分析：A和B在振动过程中恰好不发生相对滑动时，AB间静摩擦力达到最大，此时振幅最大．先以A为研究对象，根据牛顿第二定律求出加速度，再对整体研究，根据牛顿第二定律和胡克定律求出振幅．
解：当A和B在振动过程中恰好不发生相对滑动时，AB间静摩擦力达到最大．根据牛顿第二定律得：
以A为研究对象：
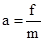
以整体为研究对象：kA=（M+m）a
联立两式得，
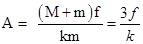
点评：本题运用牛顿第二定律研究简谐运动，既要能灵活选择研究对象，又要掌握简谐运动的特点．基础题．
练习册系列答案
相关题目
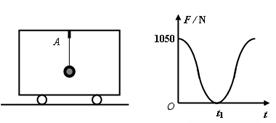
的物体在水平外力的作用下在一水平面上运动，物体和水平面间的动摩擦因数
，已知物体运动过程中的坐标与时间的关系为
（m），
（m），
。根据以上条件求：
时物体的位置坐标；
