题目内容
15.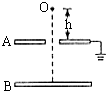 如图所示,水平放置的平行金属板A、B的距离为d,开始两板都不带电,现将电荷量为+q、质量为m的液滴从小孔正上方h处无初速度滴下,通过小孔落向B板并把电荷全部传给B板,重力加速度为g,求:
如图所示,水平放置的平行金属板A、B的距离为d,开始两板都不带电,现将电荷量为+q、质量为m的液滴从小孔正上方h处无初速度滴下,通过小孔落向B板并把电荷全部传给B板,重力加速度为g,求:(1)若第N滴在AB间恰好做匀速运动,求电容器的电容;
(2)能到达B板的液滴不会超过多少滴?
分析 (1)设第n滴液滴在A、B板间做匀速直线运动时,重力与电场力平衡,由E=$\frac{U}{d}$,U=$\frac{Q}{C}$,Q=(N-1)q,结合求解C.
(2)油滴不断从小孔滴下并附着到下板上,上下板之间就形成了电势差,也就形成了匀强电场,设最终有x个油滴可以打到下板上,即第x+1个油滴到达下极板时速度正好等于0,以后的油滴就不会打到板上了,根据动能定理即可求解.
解答 解:(1)设第N滴液滴在A、B板间做匀速直线运动,此时,板上电荷量为:Q=(n-1)q,板上电压为:U=$\frac{Q}{C}$=$\frac{(n-1)q}{C}$…①
板间电场强度为:E=$\frac{U}{d}$=$\frac{(n-1)q}{Cd}$…②
由平衡条件得:qE=mg…③
由①②③得:C=$\frac{{q}^{2}N-{q}^{2}}{mgd}$.
(2)设能够到达B板的液滴不会超过x滴,且第(x-1)滴到B板的速度恰为0,然后返回极板上,最大电荷量为:Q′=xq…④
极板间最大电压为:U′=$\frac{Q′}{C}$=$\frac{(x-1)q}{C}$…⑤
对第(x-1)滴,由动能定理得:mg(h+d)-qU′=0…⑥
由⑤⑥解得:x=$\frac{mgC(h+d)}{{q}^{2}}$+1=$\frac{N(h+d)}{d}-\frac{h}{d}$.
答:(1)若第N滴在AB间恰好做匀速运动,电容器的电容是$\frac{{q}^{2}N-{q}^{2}}{mgd}$;
(2)能到达B板的液滴不会超过$\frac{N(h+d)}{d}-\frac{h}{d}$滴.
点评 本题主要考查了动能定理在电场中的应用,要知道当油滴滴到下极板时速度刚好为零,下面的油滴就不能滴到下极板上.

| A. | 做平抛运动的物体加速度一直增大 | |
| B. | 做圆周运动的物体,其加速度一定指向圆心 | |
| C. | 不共线的两个初速度不为零的匀变速直线运动的合运动一定是匀变速运动 | |
| D. | 物体在恒力作用下做曲线运动,在相同时间内的速度变化量一定相同 |
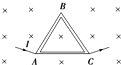 如图所示,一个边长为L、三边电阻相同的正三角形金属框放置在磁感应强度为B的匀强磁场中,若通以如图所示方向的电流(从A点流入,从C点流出),电流大小为I,则关于金属框所受安培力的情况,下列说法正确的是( )
如图所示,一个边长为L、三边电阻相同的正三角形金属框放置在磁感应强度为B的匀强磁场中,若通以如图所示方向的电流(从A点流入,从C点流出),电流大小为I,则关于金属框所受安培力的情况,下列说法正确的是( )| A. | 金属框所受安培力大小为0 | |
| B. | 金属框所受安培力大小为BIL,方向垂直AC沿纸面向上 | |
| C. | 金属框所受安培力大小为$\frac{4}{3}$BIL,方向垂直AC沿纸面向下 | |
| D. | 金属框所受安培力大小为2BIL,方向垂直AC沿纸面向上 |
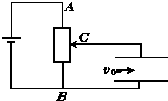 如图所示,平行板电容器的一个极板与滑动变阻器的滑动端C相连接,平行板电容器两极板间距为d.电子以速度v0从平行板电容器左侧极板正中间垂直于电场线方向射入,从平行板电容器右侧距上极板$\frac{1}{4}d$处离开电场,即沿电场方向偏移的位移y=$\frac{1}{4}d$.若使滑动变阻器的滑动端C上移,电子在平行板间运动沿电场方向偏移的位移y和运动时间t的说法中,正确的是( )
如图所示,平行板电容器的一个极板与滑动变阻器的滑动端C相连接,平行板电容器两极板间距为d.电子以速度v0从平行板电容器左侧极板正中间垂直于电场线方向射入,从平行板电容器右侧距上极板$\frac{1}{4}d$处离开电场,即沿电场方向偏移的位移y=$\frac{1}{4}d$.若使滑动变阻器的滑动端C上移,电子在平行板间运动沿电场方向偏移的位移y和运动时间t的说法中,正确的是( )| A. | 位移y增大,时间t可能变小 | B. | 位移y增大,时间t 一定增大 | ||
| C. | 位移y增大,时间t可能不变 | D. | 位移y不变,时间t一定不变 |
 巴中龙泉外国语学校物理兴趣小组想了解电阻丝的电阻与哪些因素有关.因此进行了探究,他们对某种金属材料制成的电阻丝做了如下测量,数据如图所示.
巴中龙泉外国语学校物理兴趣小组想了解电阻丝的电阻与哪些因素有关.因此进行了探究,他们对某种金属材料制成的电阻丝做了如下测量,数据如图所示.| 编号 | 金属丝直径D/mm | 金属丝直径的平方D2/mm2 | 横截面积S/mm2 | 金属丝长度L/cm | 电阻R/Ω |
| 1 | 0.30 | 0.09 | 100.00 | 14.20 | |
| 2 | 0.30 | 0.09 | 50.00 | 7.15 | |
| 3 | 0.60 | 0.36 | 100.00 | 3.60 |
A.控制变量法 B.等效替代法
C.伏安法 D.极限法
(2)通过表中数据可以分析出,该金属材料电阻丝的电阻和长度成正比.
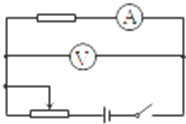
(3)如图是测量电阻丝的电阻时选择的原理图,则该同学选择该电路进行测量时,测量的电阻值比真实值偏大(选填“偏大”或者“偏小”).
(4)请写出电阻R与L、D间的关系式R=ρ$\frac{4L}{π{D}^{2}}$(金属丝的电阻率用ρ表示).根据表中数据,求出电阻率ρ=1.0×10-6Ω•m(结果保留两位有效数字).
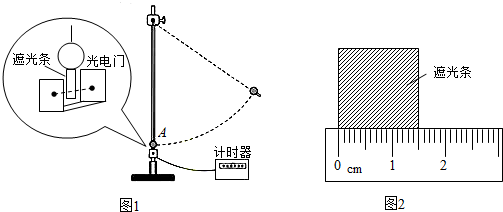
(1)用△Ep=mgh计算钢球重力势能变化的大小,式中钢球下落高度h应测量释放时的钢球球心到B之间的竖直距离.
(A)钢球在A点时的顶端
(B)钢球在A点时的球心
(C)钢球在A点时的底端
(2)用△Ek=$\frac{1}{2}$mv2计算钢球动能变化的大小,用刻度尺测量遮光条宽度,示数如图2所示,其读数为1.50cm.某次测量中,计时器的示数为0.0100s,则钢球的速度为v=1.50m/s.
(3)如表为该同学的实验结果:
他发现表中的△Ep与△Ek之间存在差异,你认为这是所测量速度为挡光片的速度,比小球速度大造成的.应该如何修正测出固定点到挡光片的距离算出小球速度即可.
| △Ep(×10-2J) | 4.892 | 9.786 | 14.69 | 19.59 | 29.38 |
| △Ek(×10-2J) | 5.04 | 10.1 | 15.1 | 20.0 | 29.8 |
 (1)在“验证机械能守恒定律”实验中,在下面所列举的该实验的几个操作步骤中,你认为没有必要进行的或者错误的步骤是BCD(填字母代号)
(1)在“验证机械能守恒定律”实验中,在下面所列举的该实验的几个操作步骤中,你认为没有必要进行的或者错误的步骤是BCD(填字母代号)