题目内容
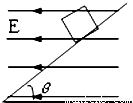
 如图所示,一带电量q=-3×10-3C,质量为m=0.4Kg的小物块处于一倾角θ=37o的光滑斜面上,当整个装置处于一水平向左的匀强电场中时,小物块恰处于静止状态.重力加速度g=10m/s2.求:
如图所示,一带电量q=-3×10-3C,质量为m=0.4Kg的小物块处于一倾角θ=37o的光滑斜面上,当整个装置处于一水平向左的匀强电场中时,小物块恰处于静止状态.重力加速度g=10m/s2.求:(1)该匀强电场的电场强度大小.(sin37o=0.6,cos37o=0.8)
(2)若该电场方向改为竖直向下后,小物块在斜面上由静止释放后的加速度是多大?小物块在斜面上运动2s,电场力做了多少功?(设斜面足够长)
分析:(1)物块受重力、支持力和电场力处于平衡,通过共点力平衡求出匀强电场的电场强度.
(2)根据牛顿第二定律求出小物块的加速度,通过位移时间公式求出位移的大小,从而求出电场力做功的大小.
(2)根据牛顿第二定律求出小物块的加速度,通过位移时间公式求出位移的大小,从而求出电场力做功的大小.
解答:解:(1)根据共点力平衡得,qE=mgtan37° 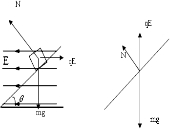
解得 E=
=1×103N/C
(2)根据牛顿第二定律得,(mg-qE) sin37°=ma
解得 a=
=1.5m/s2
通过位移时间公式得,X=
at2=
×1.5×22=3m
电场力做功 W=-qEXsin37°=-3×10-3×1×103×3×0.6=-5.4J.
答:(1)匀强电场的电场强度大小为1×103N/C
(2)电场力做功为-5.4J.

解得 E=
| 3mg |
| 4q |
(2)根据牛顿第二定律得,(mg-qE) sin37°=ma
解得 a=
| (mg-qE)sin37° |
| m |
通过位移时间公式得,X=
| 1 |
| 2 |
| 1 |
| 2 |
电场力做功 W=-qEXsin37°=-3×10-3×1×103×3×0.6=-5.4J.
答:(1)匀强电场的电场强度大小为1×103N/C
(2)电场力做功为-5.4J.
点评:解决本题的关键能够正确地受力分析,运用共点力平衡和牛顿第二定律进行求解.

练习册系列答案
相关题目
 如图所示,一带电量为+q的点电荷与均匀带电的正三角形的薄板相距为2d,+q到带电薄板的垂线通过板的几何中心,若图中a点处的合电场强度为零,正确应用等效和对称的思维方法求出带电薄板与+q在图中b点处产生的合电场强度大小为(静电力恒量为k)( )
如图所示,一带电量为+q的点电荷与均匀带电的正三角形的薄板相距为2d,+q到带电薄板的垂线通过板的几何中心,若图中a点处的合电场强度为零,正确应用等效和对称的思维方法求出带电薄板与+q在图中b点处产生的合电场强度大小为(静电力恒量为k)( ) 如图所示,一带电量为+q的点电荷与均匀带电的正三角形的薄板相距为2d,+q到带电薄板的垂线通过板的几何中心,若图中a点处的合电场强度为零,正确应用等效和对称的思维方法求出带电薄板与+q在图中b点处产生的合电场强度大小为(静电力恒量为k)( )
如图所示,一带电量为+q的点电荷与均匀带电的正三角形的薄板相距为2d,+q到带电薄板的垂线通过板的几何中心,若图中a点处的合电场强度为零,正确应用等效和对称的思维方法求出带电薄板与+q在图中b点处产生的合电场强度大小为(静电力恒量为k)( )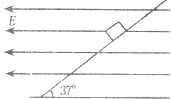 如图所示,一带电量为q、质量为m的小物块处于一倾角为37°的光滑面上,当整个装置处于一水平向左的匀强电场中时,小物块恰好处于静止状态.某时刻,电场强度突然减小为原来的
如图所示,一带电量为q、质量为m的小物块处于一倾角为37°的光滑面上,当整个装置处于一水平向左的匀强电场中时,小物块恰好处于静止状态.某时刻,电场强度突然减小为原来的