Question

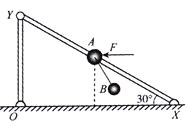
【题目】如图所示，直角三角形支架OXY在竖直平面内，XY为光滑的轻直细杆高h=l.25m的OY杆垂直于地面，XY杆与水平面夹角为30°．一个质量为m=2kg的小球A（可视为质点）穿在XY杆上，下悬一个质量为m2=1kg的小球B，对杆上小球施加一个水平向左的恒力F使其从XY杆的中点由静止开始沿杆向上运动，运动过程悬挂小球的悬线与竖直方向夹角为30°，g取10m/s2，求：

（1）小球B运动的加速度大小；

（2）小球A到达y点时的速度大小．

（3）恒力F的大小；

Answer 1

【答案】(1)10m/s2；(2)5m/s；(3)

【解析】

(1)对小球B受力分析，根据牛顿第二定律求小球B运动的加速度；

(2)对两个小球组成的整体进行受力分析，运用正交分解法，根据牛顿第二定律求F的大小；

(3)小球A做匀加速运动，根据速度位移公式求小球A到达y点的速度。

(1) 对小球B受力B球受重力、绳子拉力，根据牛顿第二定律得：

平行斜面方向：Tcos30°-m2gsin30°=m2a

垂直斜面方向：Tsin30°=m2gcos30°

联立得：a=g=10m/s2；

(2) 杆的中点与B点的距离为

根据位移公式：v2-02=2ax，

代入数据得：v=5m/s；

(3) 以两个小球组成的整体为研究对象，由牛顿第二定律得：

沿斜面方向有：Fcos30°-（m1g+m2g）sin30°=（m1+m2）a

得：。