Question

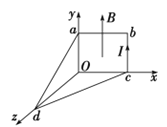
【题目】如图是一种常见的圆桌，桌面中间嵌一半径为r=1.5m、可绕中心轴转动的圆盘，桌面与圆盘面在同一水平面内且两者间缝隙可不考虑。已知桌面离地高度为h=0.8m，将一可视为质点的小碟子放置在圆盘边缘，若缓慢增大圆盘的角速度，碟子将从圆盘上甩出并滑上桌面，再从桌面飞出，落地点与桌面飞出点的水平距离是0.4m．已知碟子质量m=0.1kg，碟子与圆盘间的最大静摩擦力Fmax=0.6N．求：

（1）碟子从桌面飞出时的速度大小；

（2）碟子在桌面上运动时，桌面摩擦力对它做的功；

（3）若碟子与桌面动摩擦因数为μ=0.225，要使碟子不滑出桌面，则桌面半径至少是多少？

Answer 1

【答案】（1） （2） （3）

【解析】

（1）根据平抛运动规律：h=gt2，x=vt，

得

（2）碟子从圆盘上甩出时的速度为 ，则 ，

即

由动能定理得：

代入数据得：

（3）当物体滑到餐桌边缘时速度恰好减为零，对应的餐桌半径取最小值。
设物体在餐桌上滑动的位移为S，由动能定理有：-μmgS=0-mv2
餐桌的最小半径为 R=
可得：S=2.5m