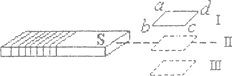Question

【题目】如图甲所示，A、B为两块相距很近的平行金属板，A、B间电压为，紧贴A板有一电子源随时间均匀地飘出质量为m，带电量为e的电子（可视为初速度为零）。在B板右侧两块平行金属板M、N间加有如图乙所示的电压，电压的变化周期，板间中线与电子源在同意以水平线上，极板长L，距偏转右边缘s处有荧光屏，已知时刻沿中线射入偏转极板间的电子恰好能射出偏转极板，假定金属外无电场，打在极板上的电子均被极板吸收，荧光屏足够大，试求：

（1）电子进入偏转极板时的速度；

（2）时刻沿中线射入偏转板间的电子刚出偏转板时与板间中线的距离；

（3）经足够长时间t（t远大于T）打到荧光屏上的电子数与电子源发射的电子数之比；

（4）电子打在荧光屏上的范围（打在荧光屏最上端和最下端的长度）。

Answer 1

【答案】（1）（2）0（3）（4）

【解析】

（1）由动能定理有

，

即

（2）由

有：

电子在电场方向先加速再减速，然后反向加速再减速，各段位移大小相等，故一个周期内，侧位移为零，电子在电场运动的两个周期内侧向位移也为零.

（3）设两极板间距为d，

，

若时刻沿中线射入偏转板间的电子恰好能射出偏转极板（不打上极板），那么

，

解得

设时刻射入的电子恰好打不到下极板，则

经时间t（t>>T）打到荧光屏上的电子数与电子源发射的电子数之比

（4）因为电子射出偏转板时，竖直方向速度为0，所以荧光屏上的范围