题目内容
8.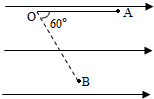 长为L的细线,上端固定,下端拴一质量为m、带电荷量为q的小球,处于如图所示的水平向右的匀强电场中,开始时,将线与小球拉成水平,然后由A点释放,小球由静止开始向下摆动,当细线转过60°角时,小球到达B点速度恰好为零.已知重力加速度为g,试求:
长为L的细线,上端固定,下端拴一质量为m、带电荷量为q的小球,处于如图所示的水平向右的匀强电场中,开始时,将线与小球拉成水平,然后由A点释放,小球由静止开始向下摆动,当细线转过60°角时,小球到达B点速度恰好为零.已知重力加速度为g,试求:(1)匀强电场的场强大小;
(2)小球到达B点时,细线对小球的拉力大小;
(3)小球从A到B运动过程中的最大动能EAB及此位置细线与水平方向夹角θ.
分析 (1)小球从A到B的过程中,重力做正功mgLsin60°,电场力做功为qUAB,动能的变化量为零,根据动能定理求解电势差UAB;根据电场强度与电势差的关系U=Ed求解场强.式中d是AB沿电场线方向的距离,d=L-Lcos60°.
(2)小球在AB间摆动时具有对称性,B处绳拉力与A处绳拉力相等,研究A处绳子的拉力得到B处绳子的拉力.在A处小球水平方向平衡,由平衡条件求解拉力
(3)速度最大,此时,切向方向合力为零,根据受力分析求的夹角,根据动能定理求得最大动能
解答 解:(1)小球由A→B过程中,由动能定理:
mgLsin60°-qUAB=0
所以UAB=$\frac{\sqrt{3}mgL}{2q}$
E=$\frac{{U}_{AB}}{L-Lcos60°}=\frac{\sqrt{3}mg}{q}$
(2)小球在AB间摆动,由对称性知,B处细线拉力与A处细线拉力相等,而在A处,由水平方向平衡有
TA=Eq=$\sqrt{3}$mg
所以TB=TA=$\sqrt{3}$mg
或在B处,沿细线方向合力为零,有
TB=Eqcos60°+mgcos30°=$\sqrt{3}$mg.
(3)假设静止释放,与水平方向的夹角为θ,速度最大,此时,切向方向合力为零
满足qEsinθ=mgcosθ
解得$tanθ=\frac{mg}{qE}=\frac{\sqrt{3}}{3}$
即θ=30°
根据动能定理可得mgLsin30°-qEL(1-os30°)=Ek-0
解得${E}_{k}=(2-\sqrt{3})mgL$
答:(1)匀强电场的场强大小为$\frac{\sqrt{3}mg}{q}$;
(2)小球到达B点时,细线对小球的拉力大小为$\sqrt{3}$mg
(3)小球从A到B运动过程中的最大动能EAB为$(2-\sqrt{3})mgL$,此位置细线与水平方向夹角θ为30.
点评 本题考查了动能定理,共点力平衡条件,电场力做功的直接应用,第(2)问题也可以直接研究B处得到,小球在B处,沿绳方向合力为零
有:FTB=Eqcos60°+mgcos30°=$\sqrt{3}mg$

 如图所示,在固定的光滑斜面上,有一重量为G的物体在一水平推力F的作用下处于静止状态.若斜面的斜角为θ,则( )
如图所示,在固定的光滑斜面上,有一重量为G的物体在一水平推力F的作用下处于静止状态.若斜面的斜角为θ,则( )| A. | F=Gtanθ | B. | F=Gsinθ | ||
| C. | 物体对斜面的压力FN=Gcosθ | D. | 物体对斜面的压力FN=Gsinθ |
| A. | 单摆的摆球振动到平衡位置时,所受的合力并不等于零 | |
| B. | 光速不变原理是:真空中的光速在不同的惯性参考系中都是相等的 | |
| C. | 不论是机械波还是电磁波的传播速度都等于波长与周期的比值 | |
| D. | 两列波相叠加产生干涉现象时,振动加强区域与减弱区域交替变化 | |
| E. | 任何波都有折射、反射和偏振现象 |
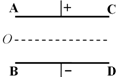 如图所示为示波管中偏转电极的示意图,相距为d、长度为L的极板AC、BD加上电压U后,可在两极板之间(设为真空)产生匀强电场.在左端距两板等距离处的O点,有一电荷量为-q、质量为m的粒子以某一速度沿与板平行射入,不计重力,下列说法正确的是( )
如图所示为示波管中偏转电极的示意图,相距为d、长度为L的极板AC、BD加上电压U后,可在两极板之间(设为真空)产生匀强电场.在左端距两板等距离处的O点,有一电荷量为-q、质量为m的粒子以某一速度沿与板平行射入,不计重力,下列说法正确的是( )| A. | 入射粒子向下偏转 | |
| B. | 入射速度大于$\frac{L}{d}\sqrt{\frac{qU}{m}}$的粒子可以射出电场 | |
| C. | 若粒子可以射出电场,则入射速度越大,动能变化越大 | |
| D. | 若粒子可以射出电场,则射出电场时速度方向的反向延长线过O点 |
 某同学用如图1所示的实验装置探究外力做功与小车动能变化的关系.
某同学用如图1所示的实验装置探究外力做功与小车动能变化的关系.
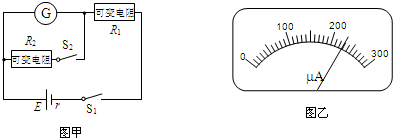
 为了测量某电池的电动势E(约3V)和内阻r(约5Ω),可供选择的器材如下:
为了测量某电池的电动势E(约3V)和内阻r(约5Ω),可供选择的器材如下: