题目内容
【题目】如图所示,光滑水平面上放着长为L=1.6m,质量为M=3.0kg的木板,一个质量为m=1.0kg的小木块放在木板的最右端,m与M之间的木擦因数μ=0.1,今对木板施加一水平向右的拉力F.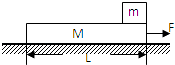
(1)施力F后,要想把木板从木块m的下方抽出来,求力F的大小应满足的条件;
(2)如果所施力F=10N,为了把木板从m的下方抽出来,此力的作用时间不得少于多少?(g取10m/s2)
【答案】
(1)解:当m刚开始滑动时,加速度a=μg,
对整体分析,F=(M+m)a=4×0.1×10N=4N.
所以F>4N时,木板才能从木块m的下方抽出来
答:力F的大小应满足的条件是F>4N
(2)解:设木块滑到木板最左端速度恰好与木板相同时,水平力作用的时间为t,相同速度v,此过程木板滑行的距离为S.
对系统:
根据动量定理得
Ft=(M+m)v ①
根据动能定理得
FS﹣μmgL= ![]() ②
②
又由牛顿第二定律得到木板加速运动的加速度为
![]() ③
③
此过程木板通过的位移为S= ![]() ④
④
联立上述四式得t=0.8s
答:力的作用时间不得少于0.8s
【解析】(1)根据牛顿第二定律求出m刚好开始滑动时,运用整体法求出拉力F的大小,从而求出拉力F的范围.(2)题中木板在恒力F的作用下由静止开始向右加速运动,滑块受摩擦力作用相对地面也向右匀加速滑动,由牛顿第二定律求出木板的加速度大于滑块的加速度.所以在力F作用时间内木板的速度必大于滑块的速度,若力F作用一段时间停止后,木块继续做匀加速运动,木板做匀减速运动,当两者的速度恰好能够相等并且木块滑到木板最左端时达到下滑的临界状态,这时木块相对于木板的位移为L,则力F作用在木板上的时间就是最短时间.对系统研究,根据动量定理列出时间与速度的关系式,根据动能定理列出木板滑行距离速度,由运动学公式列出时间与木板滑行距离与时间的关系,再联立求解时间.
【考点精析】掌握动能定理的综合应用是解答本题的根本,需要知道应用动能定理只考虑初、末状态,没有守恒条件的限制,也不受力的性质和物理过程的变化的影响.所以,凡涉及力和位移,而不涉及力的作用时间的动力学问题,都可以用动能定理分析和解答,而且一般都比用牛顿运动定律和机械能守恒定律简捷.