题目内容
如图所示为一固定的游戏轨道,左右两侧的斜直管道PA与PB分别与半径R=1cm的“8”字型圆形管道的低端圆滑连接,处于同一竖直平面内。两斜直管道的倾角相同,高度相同,粗糙程度也相同,管口A、B两处均用光滑小圆弧管连接(其长度不计,管口处切线竖直),管口到低端的竖直高度H2=0.4m,“8”字型管道内壁光滑,整个管道粗细均匀,装置固定在竖直平面内。质量m=0.5kg的小物块从距管口A的正上方H1=5m处自由下落,第一次到达最低点P处时的速度大小为10m/s,此后经管道运动到B处并竖直向上飞出,然后又再次落回,… … ,如此反复。忽略物块进入管口时因碰撞而造成的能损,忽略空气阻力,小物块视为质点,管道内径大小不计,最大静摩擦力大于滑动摩擦力,g取10m/s2。求:
(1)小物块第一次到达“8”字型管道顶端时对管道的作用力F
(2)小物块第一次离开管口B后上升的最高点距管口处的距离h
(3)小物块能离开两边槽口的总次数

(1) mV2/2–mVP2/2 =-4mgR ------------------3分
F+mg= mV2/R --------------------------3分
联合得:F=4985N ----------------------2分
(2) mg(H1-h)=2Wf --------------------------3分
mVP2/2 = mg(H1+H2)-Wf ------------------3分
或0-mVP2/2 = -mg(H2+h)-Wf
联合得:h=4.2m -----------------------2分
(3)n=mgH1/2Wf=6.25 -----------------------2分
故能离开两边槽口的总次数为6次--------2分




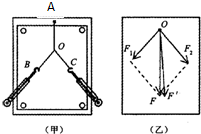 B.等效替代法
B.等效替代法