题目内容
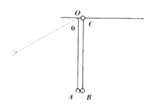
【题目】如图所示,一条长为L的细绳端系于O点,另一端系一个质量为m的小钢球![]() 视为质点
视为质点![]() ,另一条相同的细绳两端系着质量为2m的小钢球
,另一条相同的细绳两端系着质量为2m的小钢球![]() 视为质点
视为质点![]() 和质量为m的小钢球
和质量为m的小钢球![]() 视为质点
视为质点![]() ,其中C球穿过光滑的水平细杆,开始时悬线竖直,A、B两球刚好接触,现将A拉到与竖直方向成
,其中C球穿过光滑的水平细杆,开始时悬线竖直,A、B两球刚好接触,现将A拉到与竖直方向成![]() 的位置,由静止释放后与B球发生弹性正碰,已知重力加速度为g,求:
的位置,由静止释放后与B球发生弹性正碰,已知重力加速度为g,求:
![]() 、B碰撞结束时,小球B的速度
、B碰撞结束时,小球B的速度![]() ;
;
![]() 球向右运动过程中的最大高度
球向右运动过程中的最大高度![]() 。
。
【答案】(1)![]() ;(2)
;(2)![]() 。
。
【解析】
解:![]() 设小球A即将与小球B碰撞前的速度为
设小球A即将与小球B碰撞前的速度为![]() ,小球A由初始位置摆动到最低点的过程中,由机械能守恒定律可得:
,小球A由初始位置摆动到最低点的过程中,由机械能守恒定律可得:
![]()
解得:![]()
设碰撞后小球A速度为![]() ,小球B速度为
,小球B速度为![]() ,由于小球A与小球B是弹性碰撞,所以碰撞过程满足机械能守恒和动量守恒,取向右为正方向,则得:
,由于小球A与小球B是弹性碰撞,所以碰撞过程满足机械能守恒和动量守恒,取向右为正方向,则得:![]()
![]()
两式联立可得:![]()
![]() 当B向右的位置最高时,B与C水平方向的速度相等,由动量守恒可得:
当B向右的位置最高时,B与C水平方向的速度相等,由动量守恒可得:![]()
由能量守恒定律可得:![]()
联立解得:![]()
答:![]() 、B碰撞结束时,小球B的速度
、B碰撞结束时,小球B的速度![]() 为
为![]() ;
;
![]() 球向右运动过程中的最大高度
球向右运动过程中的最大高度![]() 为
为![]() 。
。

练习册系列答案
相关题目
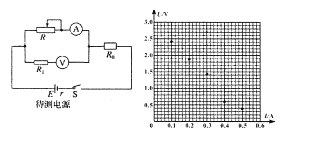
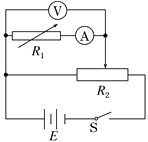
【题目】用电压表、电流表、滑动变阻器可测量一节蓄电池(电动势约为2.0V)的电动势和内阻,实验所用器材如图所示.

(1)请将左侧的实物图连接成所需的实验电路;
(2)某同学在做该实验时,调整滑动变阻器共测得了5组电流、电压的数据,如表所示.请在右侧的坐标纸中作出该电池的U﹣I图象,并根据图象得出:
电池的电动势E=_____V,内阻 r=_____Ω.
电流表读数I/A | 1.72 | 1.35 | 0.98 | 0.63 | 0.34 |
电压表读数U/V | 1.88 | 1.92 | 1.94 | 1.98 | 1.99 |