题目内容
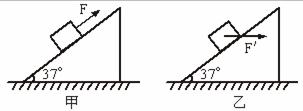
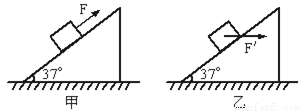
 如图甲所示,一固定的粗糙斜面的倾角为37°,一物块m=5kg在斜面上,若用F=50N的力沿斜面向上推物块,物块能沿斜面匀速上升,g=10m/s2,sin37°=0.6,cos37°=0.8.
如图甲所示,一固定的粗糙斜面的倾角为37°,一物块m=5kg在斜面上,若用F=50N的力沿斜面向上推物块,物块能沿斜面匀速上升,g=10m/s2,sin37°=0.6,cos37°=0.8.(1)求物块与斜面间的动摩擦因数μ;
(2)若将F改为水平向右推力F′(如图乙),则F′为多大时才能使物块沿斜面匀速运动.(设最大静摩擦力等于滑动摩擦力)
分析:(1)物体沿斜面匀速向上运动,合力为零,分析物体的受力情况,由平衡条件求出物体所受的支持力和摩擦力,即可由摩擦力公式f=μN,求出μ;
(2)物体匀速上滑时受重力、推力、支持力和平行斜面向下的摩擦力,根据共点力平衡条件列式求解;物体匀速上滑时受重力、推力、支持力和平行斜面向上的摩擦力,根据共点力平衡条件列式求解.
(2)物体匀速上滑时受重力、推力、支持力和平行斜面向下的摩擦力,根据共点力平衡条件列式求解;物体匀速上滑时受重力、推力、支持力和平行斜面向上的摩擦力,根据共点力平衡条件列式求解.
解答:解:(1)以物体A为研究对象,受到四个力的作用:重力G,拉力F,支持力FN,滑动摩擦力F1,物体处于平衡状态,建立如图所示直角坐标系,由共点力平衡条件得: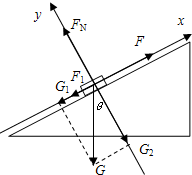
F-mgsinθ-F1=0
FN-mgcos θ=0
又 F1=μFN
解得:μ=
=
=
=0.5
(2)当物体匀速上滑时,根据平衡条件有:
平行斜面方向:F′cos37°-Gsin37°-f′=0
垂直斜面方向:N′-F′sinθ-Gcosθ=0
其中:f′=μN′
联立解得:F′=100N
当物体匀速下滑时,根据共点力平衡条件,有:
平行斜面方向:Gsin37°-F′cos37°-f′=0
垂直斜面方向:N′-F′sinθ-Gcosθ=0
其中:f′=μN′
联立解得:F′=
N=9.1N
答:(1)物块与斜面间的动摩擦因数μ为0.5;
(2)F′为100N时沿斜面向上匀速运动;F′为9.1N时沿斜面向下匀速运动.

F-mgsinθ-F1=0
FN-mgcos θ=0
又 F1=μFN
解得:μ=
| F1 |
| FN |
| F-mgsin37° |
| mgcos37° |
| 50-50×0.6 |
| 50×0.8 |
(2)当物体匀速上滑时,根据平衡条件有:
平行斜面方向:F′cos37°-Gsin37°-f′=0
垂直斜面方向:N′-F′sinθ-Gcosθ=0
其中:f′=μN′
联立解得:F′=100N
当物体匀速下滑时,根据共点力平衡条件,有:
平行斜面方向:Gsin37°-F′cos37°-f′=0
垂直斜面方向:N′-F′sinθ-Gcosθ=0
其中:f′=μN′
联立解得:F′=
| 100 |
| 11 |
答:(1)物块与斜面间的动摩擦因数μ为0.5;
(2)F′为100N时沿斜面向上匀速运动;F′为9.1N时沿斜面向下匀速运动.
点评:本题关键对物体受力分析后,根据平衡条件并结合正交分解法多次列式求解,不难,但要有耐心.

练习册系列答案
相关题目
 (如图乙),则
(如图乙),则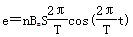 ,其中Bm为磁感应强度的最大值,T为磁场变化的周期.不计灯丝电阻随温度的变化,求:
,其中Bm为磁感应强度的最大值,T为磁场变化的周期.不计灯丝电阻随温度的变化,求: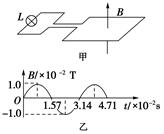
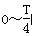 的时间内,通过小灯泡的电荷量.
的时间内,通过小灯泡的电荷量.