题目内容
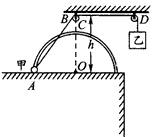
如图所示,一个半径R为0.6 m的光滑半圆细环竖直放置并固定在水平桌面上,O为圆心,A为半圆环左边最低点,C为半圆环最高点。环上套有一个质量为1 kg的小球甲,甲可以沿着细环轨道在竖直平面内做圆周运动,在水平桌面上方固定了B、D两个定滑轮,定滑轮的大小不计,与半圆环在同一竖直平面内,它们距离桌面的高度均为h=0.8米,滑轮B恰好在O点的正上方。现通过两个定滑轮用一根不可以伸长的细线将甲与一个质量为2 kg的物体乙连在一起。一开始,用手托住乙,使小球甲处于A点,细线伸直,当乙由静止释放后。(g取10m/s2)
(1)甲运动到C点时的速度大小是多少?
(2)甲、乙速度相等时,它们的速度大小是多少?
(1)甲运动到C点时的速度大小是多少?
(2)甲、乙速度相等时,它们的速度大小是多少?
解:(1)由几何知识可得:LAB=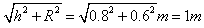
甲运动到C点时,乙的速度为零,由动能定理可得: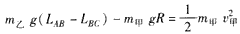
解得:v甲=4.5 m/s
(2)当连接甲球的细线与圆环相切时,甲、乙速度相等,此时甲球到达A'点,离开桌面的距离为d,则: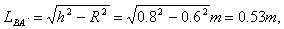
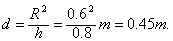
由动能定理得:m乙g(LAB-LBA')-m甲gd=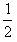 (m甲+m乙)v共2
(m甲+m乙)v共2
联立解得:v共=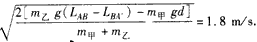
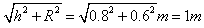
甲运动到C点时,乙的速度为零,由动能定理可得:
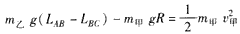
解得:v甲=4.5 m/s
(2)当连接甲球的细线与圆环相切时,甲、乙速度相等,此时甲球到达A'点,离开桌面的距离为d,则:
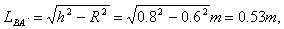
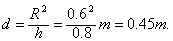
由动能定理得:m乙g(LAB-LBA')-m甲gd=
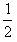 (m甲+m乙)v共2
(m甲+m乙)v共2 联立解得:v共=
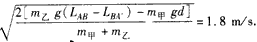

练习册系列答案
相关题目
 如图所示,一个半径R=0.80m的
如图所示,一个半径R=0.80m的 如图所示,一个半径R=0.80m的四分之一光滑圆形轨道固定在竖直平面内,底端切线水平,距地面高度H=1.25m.在轨道底端放置一个质量mB=0.30kg的小球B.另一质量mA=0.10kg的小球A(两球均视为质点)由圆形轨道顶端无初速释放,运动到轨道底端与球B发生正碰,碰后球B水平飞出,其落到水平地面时的水平位移S=0.80m.忽略空气阻力,重力加速度g取10m/s2,求:
如图所示,一个半径R=0.80m的四分之一光滑圆形轨道固定在竖直平面内,底端切线水平,距地面高度H=1.25m.在轨道底端放置一个质量mB=0.30kg的小球B.另一质量mA=0.10kg的小球A(两球均视为质点)由圆形轨道顶端无初速释放,运动到轨道底端与球B发生正碰,碰后球B水平飞出,其落到水平地面时的水平位移S=0.80m.忽略空气阻力,重力加速度g取10m/s2,求: 如图所示,一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与竖直方向夹角θ=60°,C为轨道最低点,D为轨道最高点.一个质量m=0.50kg的小球(视为质点)从空中A点以v0=4.0m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.重力加速度g取10m/s2.试求:
如图所示,一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与竖直方向夹角θ=60°,C为轨道最低点,D为轨道最高点.一个质量m=0.50kg的小球(视为质点)从空中A点以v0=4.0m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.重力加速度g取10m/s2.试求: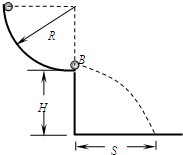 如图所示,一个半径R=0.80m的四分之一光滑圆形轨道固定在竖直平面内,底端切线水平,距地面高度H=1.25m.在轨道底端放置一个质量mB=0.30kg的小球B.另一质量mA=0.10kg的小球A(两球均视为质点)由圆形轨道顶端无初速释放,运动到轨道底端与球B发生正碰,碰后球B水平飞出,其落到水平地面时的水平位移S=0.80m.忽略空气阻力,重力加速度g取10m/s2,求:
如图所示,一个半径R=0.80m的四分之一光滑圆形轨道固定在竖直平面内,底端切线水平,距地面高度H=1.25m.在轨道底端放置一个质量mB=0.30kg的小球B.另一质量mA=0.10kg的小球A(两球均视为质点)由圆形轨道顶端无初速释放,运动到轨道底端与球B发生正碰,碰后球B水平飞出,其落到水平地面时的水平位移S=0.80m.忽略空气阻力,重力加速度g取10m/s2,求: (2008?上海模拟)如图所示,一个半径R、质量m的均匀薄圆盘处在竖直方向上,可绕过其圆心O的水平转动轴无摩擦转动,现在其右侧挖去圆心与转轴O等高、直径为R的一个圆,然后从图示位置将其静止释放,则剩余部分
(2008?上海模拟)如图所示,一个半径R、质量m的均匀薄圆盘处在竖直方向上,可绕过其圆心O的水平转动轴无摩擦转动,现在其右侧挖去圆心与转轴O等高、直径为R的一个圆,然后从图示位置将其静止释放,则剩余部分