��Ŀ����
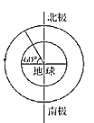
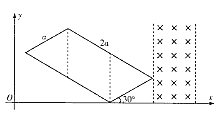
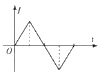
����Ŀ����ͼ���ռ���ڷ�����ֱ���£�xOyΪ�⻬��Եˮƽ���棩�Ĵų�����![]() ���Ÿ�Ӧǿ�ȵĴ�СΪB0��
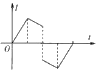
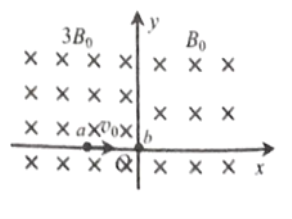
���Ÿ�Ӧǿ�ȵĴ�СΪB0��![]() ���Ÿ�Ӧǿ�ȵĴ�СΪ3B0��һ�������硢����Ϊm�Ľ���С��a��ˮƽ�����ٶ��뾲ֹ��O�㡢�����Ϊq��q��0��������Ϊ2m����״��С��a��ȫһ���Ľ���С��b������ȫ������������:����������ײǰ���������������ã�
���Ÿ�Ӧǿ�ȵĴ�СΪ3B0��һ�������硢����Ϊm�Ľ���С��a��ˮƽ�����ٶ��뾲ֹ��O�㡢�����Ϊq��q��0��������Ϊ2m����״��С��a��ȫһ���Ľ���С��b������ȫ������������:����������ײǰ���������������ã�
��1����ײ����ʱ����С��a��b�ٶ�
��2������ײ������b����ٶȷ����ٴ���x���������ʱ��
��3����ʱb����O���ľ���.
���𰸡���1�� ![]() ����������
����������![]() ���������ң�2��
���������ң�2��![]() ��3��
��3��![]()
��������
(1)�ɵ�����ײ��
mv0=mv1+2mv2
![]() =
=![]() +
+![]()
��ã�
![]() ����������
����������
![]() ����������
����������
(2)����������ײʱ��������·ֲ���a��b����![]() ������b�ڴų���������Բ���˶���
������b�ڴų���������Բ���˶���
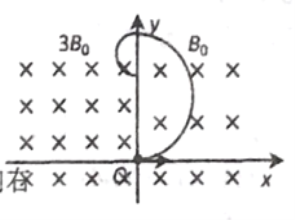
��x��0��������:
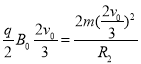
��x����������
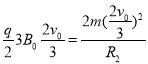
�����ٶȷ���ת��![]() ʱ�������ʱ��Ϊ��
ʱ�������ʱ��Ϊ��
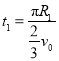
�����ٶȷ�����ת��![]() ʱ�������ʱ��Ϊ��
ʱ�������ʱ��Ϊ��
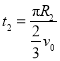
������������ʱ��Ϊ��
t0=t1+t2=![]()
(3)������O��������
d0=2��R1-R2��=![]()

��ϰ��ϵ�д�
 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д� ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
�����Ŀ