题目内容
17.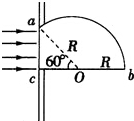 折射率n=2的透明体,其横截面如图所示,ab是一半径为R的圆弧,ac边与bc边垂直,∠aoc=60°.当一束平行黄色光垂直照射到ac边上后,ab弧的外表面只有一部分是黄亮的,而其余是暗的,求其黄亮部分的弧长是多少?
折射率n=2的透明体,其横截面如图所示,ab是一半径为R的圆弧,ac边与bc边垂直,∠aoc=60°.当一束平行黄色光垂直照射到ac边上后,ab弧的外表面只有一部分是黄亮的,而其余是暗的,求其黄亮部分的弧长是多少?
分析 根据折射定律求出临界角的大小,通过几何关系得出有黄光投射出去所对应的圆心角,从而求出其弧长.
解答  解:由题意作光路图如图所示,该介质的临界角是C.则
解:由题意作光路图如图所示,该介质的临界角是C.则
sinC=$\frac{1}{n}$=$\frac{1}{2}$,得 C=30°
如图,在α≥30°时,均发生全反射,图中d点为入射角等于临界角的临界点,所以只有bd部分有黄光透射出,
黄亮部分弧长为 s=R×$\frac{π}{6}$=$\frac{πR}{6}$
答:黄亮部分的弧长是$\frac{πR}{6}$.
点评 本题对数学几何能力考查要求较高,关键掌握全反射的条件,运用折射定律和几何知识结合进行求解.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
7. 如图所示,A、B、C是匀强电场中的三点,三点的电势分别为φA=10V,φB=4V,φC=-2V,∠A=30°,∠B=90°,AC=4$\sqrt{3}$cm,可确定该匀强电场的场强大小为( )
如图所示,A、B、C是匀强电场中的三点,三点的电势分别为φA=10V,φB=4V,φC=-2V,∠A=30°,∠B=90°,AC=4$\sqrt{3}$cm,可确定该匀强电场的场强大小为( )
 如图所示,A、B、C是匀强电场中的三点,三点的电势分别为φA=10V,φB=4V,φC=-2V,∠A=30°,∠B=90°,AC=4$\sqrt{3}$cm,可确定该匀强电场的场强大小为( )
如图所示,A、B、C是匀强电场中的三点,三点的电势分别为φA=10V,φB=4V,φC=-2V,∠A=30°,∠B=90°,AC=4$\sqrt{3}$cm,可确定该匀强电场的场强大小为( )| A. | 18V/m | B. | 12$\sqrt{3}$V/m | C. | 100$\sqrt{3}$V/m | D. | 200V/m |
2.自世界上第一颗人造卫星以来,人类的活动范围逐步扩展,现在已成功地把人造天体送到火星上漫步,我国也已实现载人航天飞行,并着手实施登月计划.下列有关人造天体的说法中正确的是( )
| A. | 卫星的轨道越高,其运转速度越大,周期越大 | |
| B. | 若地球没有自转,地球将没有同步卫星 | |
| C. | 卫星的质量一定时,轨道半径越大,它需要的向心力越大 | |
| D. | 做匀速圆周运动的载人空间站中,宇航员仍受重力的作用,但所受合外力为零 |
9.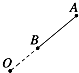 如图所示,导体棒AB长2R,绕O点以角速度ω沿逆时针方向匀速转动,OB为R,且OBA三点在一直线上,有一匀强磁场磁感应强度为B,充满转动平面且与转动平面垂直,那么AB两端的电势差大小为( )
如图所示,导体棒AB长2R,绕O点以角速度ω沿逆时针方向匀速转动,OB为R,且OBA三点在一直线上,有一匀强磁场磁感应强度为B,充满转动平面且与转动平面垂直,那么AB两端的电势差大小为( )
 如图所示,导体棒AB长2R,绕O点以角速度ω沿逆时针方向匀速转动,OB为R,且OBA三点在一直线上,有一匀强磁场磁感应强度为B,充满转动平面且与转动平面垂直,那么AB两端的电势差大小为( )
如图所示,导体棒AB长2R,绕O点以角速度ω沿逆时针方向匀速转动,OB为R,且OBA三点在一直线上,有一匀强磁场磁感应强度为B,充满转动平面且与转动平面垂直,那么AB两端的电势差大小为( )| A. | $\frac{3}{2}$BωR2 | B. | 2BωR2 | C. | 4BωR2 | D. | 6BωR2 |
6.机械能守恒定律的内容是:“在只有重力或弹力做功的物体系内,动能与势能可以相互转化,而总的机械能保持不变.”下列对机械能守恒定律的理解中正确的是( )
| A. | “势能”包括重力势能和弹性势能 | |
| B. | 物体系“总的机械能”包括动能、重力势能和弹性势能 | |
| C. | 物体系总的机械能可以变为其他值,但最终又变回原来的值 | |
| D. | 物体系机械能守恒与否与零重力势能平面的选取有关 |
7.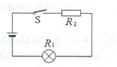 如图所示,为一环境温度监控电器,R1为灯泡,R2为半导体材料制成的热敏电阻(电阻随温度升高而变小),当环境温度降低时则有( )
如图所示,为一环境温度监控电器,R1为灯泡,R2为半导体材料制成的热敏电阻(电阻随温度升高而变小),当环境温度降低时则有( )
 如图所示,为一环境温度监控电器,R1为灯泡,R2为半导体材料制成的热敏电阻(电阻随温度升高而变小),当环境温度降低时则有( )
如图所示,为一环境温度监控电器,R1为灯泡,R2为半导体材料制成的热敏电阻(电阻随温度升高而变小),当环境温度降低时则有( )| A. | 灯泡的亮度变亮,电路中消耗的总功率P变小 | |
| B. | 灯泡的亮度变亮,电路中消耗的总功率P变大 | |
| C. | 灯泡的亮度变暗,电路中消耗的总功率P变小 | |
| D. | 灯泡的亮度变暗,电路中消耗的总功率P变大 |
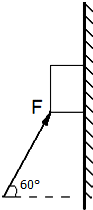 重力G=36N的物体,与竖直墙壁间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,现用与水平方向夹角成θ=60°的斜向上的推力F拖住物体.
重力G=36N的物体,与竖直墙壁间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,现用与水平方向夹角成θ=60°的斜向上的推力F拖住物体.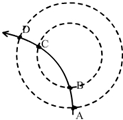 带电量为1.0×10-2C的粒子,在电场中先后飞经A,B两点,飞经A点时的动能为100J,飞经B点时的动能为40J,已知A点的电势为-700V,如图所示,求:
带电量为1.0×10-2C的粒子,在电场中先后飞经A,B两点,飞经A点时的动能为100J,飞经B点时的动能为40J,已知A点的电势为-700V,如图所示,求: