题目内容
【题目】如图所示,物体在离斜面底端5m处由静止开始下滑,然后滑上由小圆弧(长度忽略)与斜面连接的水平面上,若斜面及水平面的动摩擦因数均为0.4,斜面倾角为37°,则物体能在水平面上滑行多远?![]()
【答案】解:物体在斜面上受重力mg、支持力FN1、滑动摩擦力Ff1的作用,沿斜面加速下滑,在水平面上减速直到静止.
方法一:对物体在斜面上的受力分析如图甲所示,可知物体下滑阶段:
FN1=mgcos37°
故Ff1=μFN1=μmgcos37°
由动能定理得
mgsin37°·l1-μmgcos37°·l1= ![]() ①
①
在水平面上的运动过程中,受力分析如图乙所示
Ff2=μFN2=μmg
由动能定理得
-μmg·l2=0- ![]() ②
②
由①②两式可得
l2= ![]() l1=
l1= ![]() ×5m=3.5m
×5m=3.5m
方法二:物体受力分析同上,物体运动的全过程中,初、末状态的速度均为零,对全过程运用动能定理有
mgsin37°·l1-μmgcos37°·l1-μmg·l2=0
得l2= ![]() l1=
l1= ![]() ×5m=3.5m
×5m=3.5m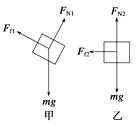
【解析】此题属于典型问题,虽然物体与接触面之间的滑动摩擦因数都相同,但斜面上和平面上物体所受摩擦力的大小不同,在整个的运动过程中物体由静止出发指导最终静止,可得出动能的变化量为零,而在整个的运动过程中只有重力和摩擦力对物体做功,故总功为零,建立方程进行求解。

练习册系列答案
相关题目