题目内容
9.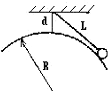 如图所示,质量为m的小球,用一根长为L的细绳吊起来,放在半径为R的光滑的球体表面上,由悬点到球面的最小距离为d.则小球对球面的压力大小为$\frac{mgR}{d+R}$,绳的张力大小为$\frac{mgL}{d+R}$.
如图所示,质量为m的小球,用一根长为L的细绳吊起来,放在半径为R的光滑的球体表面上,由悬点到球面的最小距离为d.则小球对球面的压力大小为$\frac{mgR}{d+R}$,绳的张力大小为$\frac{mgL}{d+R}$.
分析 对小球进行受力分析,由共点力的平衡条件可得出小球的受力情况,再由牛顿第三定律得出对球面的压力及绳子的拉力.
解答  解:受力分析如图所示:
解:受力分析如图所示:
由图可知,力三角形△G'NA∽△TOA
则有:$\frac{mg}{d+R}=\frac{T}{L}$
$\frac{mg}{d+R}=\frac{N}{R}$
N=$\frac{mgR}{d+R}$
T=$\frac{mgL}{d+R}$
故由牛顿第三定律可得小球对球面的压力$\frac{mgR}{d+R}$;绳子的拉力为$\frac{mgL}{d+R}$.
故答案为:$\frac{mgR}{d+R}$,$\frac{mgL}{d+R}$.
点评 此题考查共点力平衡,请记住本题,本题是采用相似三角形来处理的比较典型的题目.

练习册系列答案
相关题目
20.如图所示,一线圈处在磁场中,以下可以产生感应电流的是( )


| A. | 线圈在磁场中保持静止 | B. | 线圈在磁场中绕ab边转动 | ||
| C. | 线圈在磁场中绕ad边转动 | D. | 线圈在磁场中绕dc边转动 |
17.关于电场线,下列说法正确的是( )
| A. | 电场线和磁感线可以从演示实验中观察到 | |
| B. | 电场线是直线的电场一定是匀强电场 | |
| C. | 电场线越密的地方,电场强度越大 | |
| D. | 带电粒子在电场力作用下一定沿电场线的方向运动 |
1.伽利略和牛顿都是物理学发展史上最伟大的科学家,巧合的是牛顿就出生在伽利略去世后的第二年.下列说法中正确的是( )
| A. | 伽利略的理想斜面实验,说明了物体的运动需要力来维持 | |
| B. | 牛顿在伽利略等人研究的基础上总结提出的惯性定律 | |
| C. | 亚里士多德通过逻辑推理,认为从同一高度自由落下的重物与轻物下落一样快 | |
| D. | 亚里士多德认为物体都具有保持原来运动状态的属性,即惯性 |


 一根长为L的丝线吊着一质量为m,带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成θ角,(重力加速度为g),则小球带正电荷 (正电荷、负电荷、任一种电荷),匀强电场的电场强度的大小为$\frac{mgtanθ}{q}$.
一根长为L的丝线吊着一质量为m,带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成θ角,(重力加速度为g),则小球带正电荷 (正电荷、负电荷、任一种电荷),匀强电场的电场强度的大小为$\frac{mgtanθ}{q}$. 在用单摆测重力加速度的实验中,测得单摆摆角很小时,完成n次全振动时间为t,用毫米刻度尺测得摆线长为l,用螺旋测微器测得摆球直径为d.
在用单摆测重力加速度的实验中,测得单摆摆角很小时,完成n次全振动时间为t,用毫米刻度尺测得摆线长为l,用螺旋测微器测得摆球直径为d. 如图所示,两根足够长的直金属导轨MN、PQ平行放里在倾角为θ的绝缘斜面上,两导轨间距为L. M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于匀强磁场中,磁场方向垂直于斜面向上.导轨和金属杆的电阻可忽略.让金属杆ab沿导轨由静止开始下滑,经过足够长的时间后,金属杆达到最大速度vm,在这个过程中,电阻R上产生的热量为Q.导轨和金属杆接触良好,它们之间的动摩擦因数为μ,且μ<tanθ.已知重力加速度为g.
如图所示,两根足够长的直金属导轨MN、PQ平行放里在倾角为θ的绝缘斜面上,两导轨间距为L. M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于匀强磁场中,磁场方向垂直于斜面向上.导轨和金属杆的电阻可忽略.让金属杆ab沿导轨由静止开始下滑,经过足够长的时间后,金属杆达到最大速度vm,在这个过程中,电阻R上产生的热量为Q.导轨和金属杆接触良好,它们之间的动摩擦因数为μ,且μ<tanθ.已知重力加速度为g.