题目内容
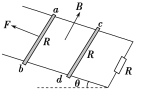
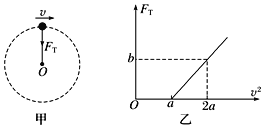
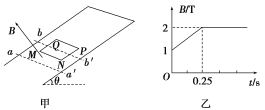
【题目】如图甲所示，足够长的粗糙斜面与水平面成θ＝
固定放置，斜面上平行虚线aa′和bb′之间有垂直斜面向上的有界匀强磁场，间距为d＝1m，磁感应强度B随时间t变化规律如图乙所示。现有一质量为m＝0.1kg，总电阻为R＝10Ω，边长也为d＝1m的正方形金属线圈MNPQ，其初始位置有一半面积位于磁场中，在t＝0时刻，线圈恰好能保持静止，此后在t＝0.25s时，线圈开始沿斜面下滑，下滑过程中线圈MN边始终与虚线aa′保持平行。已知线圈完全进入磁场前已经开始做匀速直线运动。求：（取sin＝0.6，cos＝0.8，g＝10m/s2）
(1)前0.25s内通过线圈某一截面的电量；
(2)线圈与斜面间的动摩擦因数；
(3)线圈从开始运动到通过整个磁场的过程中，电阻上产生的焦耳热。
【答案】(1)0.05C(2)0.25(3)0.55J
【解析】
(1)0.25s内，根据法拉第电磁感应定律，有
感应电流：
则0.25s内通过线圈某一截面的电量：
q=I·Δt=0.2×0.25 C=0.05C
(2)根据楞次定律，线圈内感应电流为顺时针方向。0.25s时，线圈开始沿斜面下滑。在开始下滑前有：
mgsin
=μmgcos＋BId
代入数据得：
0.6=μ×0.8＋2×0.2×1
解得：
μ=0.25
(3)设线圈最后匀速运动时的速度为v，感应电动势E=Bdv①
感应电流
②
安培力F安=BId③
联立①②③得
匀速运动时，对线圈根据平衡条件得
代入数据得：
解得
v=1m/s
根据能量守恒定律，有
代入数据：
解得：
Q=0.55J
练习册系列答案
相关题目
