题目内容
3. 如图所示,用已知力F拉着叠放在-起的A、B两块一起沿粗糙斜面匀速向上滑行,已知A的质量为2m,B的质量为m.斜面倾角为已知数,求:
如图所示,用已知力F拉着叠放在-起的A、B两块一起沿粗糙斜面匀速向上滑行,已知A的质量为2m,B的质量为m.斜面倾角为已知数,求:(1)A与斜面的摩擦系数
(2)B受到的摩擦力大小和方向.
分析 (1)对AB整体分析,根据共点力平衡求出斜面对A的滑动摩擦力大小,根据滑动摩擦力公式求出A与斜面间的动摩擦因数.
(2)隔离对B分析,根据共点力平衡求出B所受的静摩擦力大小和方向.
解答 解:(1)对整体分析,根据共点力平衡得:F=3mgsinθ+f,
解得滑动摩擦力为:f=F-3mgsinθ,
支持力为:N=3mgcosθ,
则动摩擦因数为:$μ=\frac{f}{N}=\frac{F-3mgsinθ}{3mgcosθ}$.
(2)隔离对B分析,根据共点力平衡得为:fB=mgsinθ,
方向沿斜面向上.
答:(1)A与斜面的摩擦系数为$\frac{F-3mgsinθ}{3mgcosθ}$;
(2)B受到的摩擦力大小为mgsinθ,方向沿斜面向上.
点评 解决本题的关键能够正确地受力分析,运用共点力平衡进行求解,掌握整体法和隔离法的灵活运用.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
12.一个做初速度为零的匀加速直线运动的物体,它在第1s末,第2s末,第3s末的瞬时速度之比是( )
| A. | 1:1:1 | B. | 1:3:5 | C. | 12:22:32 | D. | 1:2:3 |
13. 分别标有“6V 6W”、“6V 12W”字样的两灯泡L1、L2按甲、乙两图方式理解后接入12V的电路中,L1、L2均正常发光.以下判断正确的是( )
分别标有“6V 6W”、“6V 12W”字样的两灯泡L1、L2按甲、乙两图方式理解后接入12V的电路中,L1、L2均正常发光.以下判断正确的是( )
 分别标有“6V 6W”、“6V 12W”字样的两灯泡L1、L2按甲、乙两图方式理解后接入12V的电路中,L1、L2均正常发光.以下判断正确的是( )
分别标有“6V 6W”、“6V 12W”字样的两灯泡L1、L2按甲、乙两图方式理解后接入12V的电路中,L1、L2均正常发光.以下判断正确的是( )| A. | R1=3 R2=6Ω | |
| B. | R1=6Ω R2=2Ω | |
| C. | R1比R2消耗的功率大 | |
| D. | 甲电路消耗的总功率比乙电路消耗的总功率大 |
 如图所示为一个多用电表的原理图.已知灵敏电流表的内阻RR=300Ω,满偏电流1mA.多用电表电流挡量程为100mA,电压档量程为15V,电池的电动势1.5V,内阻未知,则R1=3.03Ω,R3=147Ω,此多用电表欧姆挡的中间刻度电阻值为15Ω.
如图所示为一个多用电表的原理图.已知灵敏电流表的内阻RR=300Ω,满偏电流1mA.多用电表电流挡量程为100mA,电压档量程为15V,电池的电动势1.5V,内阻未知,则R1=3.03Ω,R3=147Ω,此多用电表欧姆挡的中间刻度电阻值为15Ω.
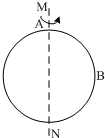 美国宇航局2015年7月24日0时(北京时间)宣布,可能发现了“另一个地球”-开普勒-452b,它距离地球1400光年.如果将开普勒-452b简化成如图所示的模型:MN为该星球的自转轴线,A、B是该星球表面上的两点(A在极地,B在赤道上);现在A、B两点各放置一质量为m的物体,用精密弹簧秤在A点称量物体,平衡时其示数为F,在B点称量物体,平衡时其示数为99.9%F,已知该星球的半径为R,试求:
美国宇航局2015年7月24日0时(北京时间)宣布,可能发现了“另一个地球”-开普勒-452b,它距离地球1400光年.如果将开普勒-452b简化成如图所示的模型:MN为该星球的自转轴线,A、B是该星球表面上的两点(A在极地,B在赤道上);现在A、B两点各放置一质量为m的物体,用精密弹簧秤在A点称量物体,平衡时其示数为F,在B点称量物体,平衡时其示数为99.9%F,已知该星球的半径为R,试求: 如图所示,物体A在水平推力F=400N的作用下,恰好沿倾斜角θ=60°的斜面匀速下滑,物体A受到的重力为400N.求:
如图所示,物体A在水平推力F=400N的作用下,恰好沿倾斜角θ=60°的斜面匀速下滑,物体A受到的重力为400N.求: 一质量为m的木块在拉力F的作用下,沿水平地面作匀速直线运动,如图所示,F与水平面的夹角a=30°,木块与地面间的动摩擦因数为μ,求拉力F的大小?
一质量为m的木块在拉力F的作用下,沿水平地面作匀速直线运动,如图所示,F与水平面的夹角a=30°,木块与地面间的动摩擦因数为μ,求拉力F的大小?