题目内容
 倾角θ=37°,质量M=5kg的粗糙斜面位于水平地面上,质量m=2kg的木块置于斜面顶端,从静止开始匀加速下滑,经t=2s到达底端,运动路程L=4m,在此过程中斜面保持静止(取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8),求:
倾角θ=37°,质量M=5kg的粗糙斜面位于水平地面上,质量m=2kg的木块置于斜面顶端,从静止开始匀加速下滑,经t=2s到达底端,运动路程L=4m,在此过程中斜面保持静止(取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8),求:(1)地面对斜面的摩擦力;
(2)斜面对地面的压力大小.
分析:(1)木块匀加速下滑,可由位移公式先求出加速度;再对物体受力分析后,根据牛顿第二定律列式,可进一步求出斜对物体的摩擦力,对斜面体受力分析,由共点力平衡条件可列式求出地面对斜面体的摩擦力;
(2)对斜面体受力分析,由共点力平衡条件可列式求出支持力.
(2)对斜面体受力分析,由共点力平衡条件可列式求出支持力.
解答:解:(1)木块做匀加速运动,由 L=
at2得:
可求 a=
=
=2m/s2;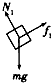
对木块受力如图①.
由牛顿第二定律
N1=mgcos37°=2×10×0.8=16N ②
mgsin37°-f1=ma ③
则得,f1=mgsin37°-ma=2×10×0.6-2×2=8N
对斜面受力如图 ④.
地面对斜面摩擦力,根据平衡条件得:
f+f1cos37°=N1′sin 37° ⑤
代入解得,f=3.2N,方向水平向左.
(2)地面对斜面的支持力N=Mg+N1′cos37°+f1′sin37°⑥
代入解得,N=67.6N
由牛顿第三定律,斜面对地面的压力大小为67.6N
答:
(1)地面对斜面的摩擦力大小为3.2N,方向水平向左;
(2)斜面对地面的压力大小是67.6N.
| 1 |
| 2 |
可求 a=
| 2L |
| t2 |
| 2×4 |
| 22 |

对木块受力如图①.
由牛顿第二定律
N1=mgcos37°=2×10×0.8=16N ②
mgsin37°-f1=ma ③
则得,f1=mgsin37°-ma=2×10×0.6-2×2=8N

对斜面受力如图 ④.
地面对斜面摩擦力,根据平衡条件得:
f+f1cos37°=N1′sin 37° ⑤
代入解得,f=3.2N,方向水平向左.
(2)地面对斜面的支持力N=Mg+N1′cos37°+f1′sin37°⑥
代入解得,N=67.6N
由牛顿第三定律,斜面对地面的压力大小为67.6N
答:
(1)地面对斜面的摩擦力大小为3.2N,方向水平向左;
(2)斜面对地面的压力大小是67.6N.
点评:本题是加速度不同的连接体问题,采用隔离法进行研究,也可能运用整体法进行求解:若用整体法可这样列式:
对整体受力分析如图:
f=ma cos37°,(M+m)g-N=masin37°.
对整体受力分析如图:
f=ma cos37°,(M+m)g-N=masin37°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
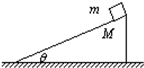 倾角θ=37°,质量M=5kg的粗糙斜面体位于水平地面上.质量m=2kg的木块置于斜面体顶端,从静止开始匀加速下滑,经t=2s到达底端,运动路程L=4m,在此过程中斜面体保持静止(sin37°=0.6,cos37°=0.8,g取10m/s2).求:
倾角θ=37°,质量M=5kg的粗糙斜面体位于水平地面上.质量m=2kg的木块置于斜面体顶端,从静止开始匀加速下滑,经t=2s到达底端,运动路程L=4m,在此过程中斜面体保持静止(sin37°=0.6,cos37°=0.8,g取10m/s2).求: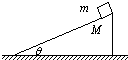 倾角θ=37°,质量M=5kg的粗糙斜面位于水平地面上.质量m=2kg的木块置于斜顶端,从静止开始匀加速下滑,经t=2s到达底端,运动路程L=4m,在此过程中斜面保持静止(sin37°=0.6,cos37°=0.8).求:
倾角θ=37°,质量M=5kg的粗糙斜面位于水平地面上.质量m=2kg的木块置于斜顶端,从静止开始匀加速下滑,经t=2s到达底端,运动路程L=4m,在此过程中斜面保持静止(sin37°=0.6,cos37°=0.8).求: 已知足够长的斜面倾角θ=37°,质量m=l0kg的物体,在斜面底部受到沿斜面向上的力F=100N作用,由静止开始运动,物体在前2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,取g=10m/s2)求:
已知足够长的斜面倾角θ=37°,质量m=l0kg的物体,在斜面底部受到沿斜面向上的力F=100N作用,由静止开始运动,物体在前2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,取g=10m/s2)求: