题目内容
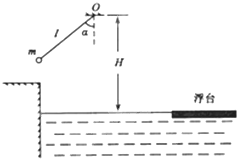 在游乐节目中,选手需借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量m=60kg的质点,选手抓住绳由静止开始摆动,绳长l=2m,此时绳与竖直方向夹角α=53°,绳的悬挂点O距水面的高度为H=3m.不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深.取重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.
在游乐节目中,选手需借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量m=60kg的质点,选手抓住绳由静止开始摆动,绳长l=2m,此时绳与竖直方向夹角α=53°,绳的悬挂点O距水面的高度为H=3m.不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深.取重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.(1)求选手摆到最低点时的速度大小;
(2)求选手摆到最低点时对绳拉力的大小F;
(3)若选手摆到最低点时松手,小明认为绳越长,在浮台上的落点距岸边越远;小阳却认为绳越短,落点距岸边越远,请通过推算说明你的观点.
分析:(1)在摆动过程中,机械能是守恒的,应用机械能守恒定律求出运动到最低点时的速度.
(2)再用牛顿运动定律结合圆周运动的向心力求出绳子对选手的拉力,最后用牛顿第三定律求出选手对绳子的拉力.
(3)对平抛运动沿水平和竖直两个方向进行分解,水平方向上是匀速直线运动,竖直方向上时自由落体运动,分别列出位移式子,联立后进行数学分析,得出当l=1.5m时,水平方向有最大值.
(2)再用牛顿运动定律结合圆周运动的向心力求出绳子对选手的拉力,最后用牛顿第三定律求出选手对绳子的拉力.
(3)对平抛运动沿水平和竖直两个方向进行分解,水平方向上是匀速直线运动,竖直方向上时自由落体运动,分别列出位移式子,联立后进行数学分析,得出当l=1.5m时,水平方向有最大值.
解答:解:(1)选手摆到最低点的过程中,机械能守恒,有:mgl(1-cosα)=
mv2
代入数据解得:v=
=
m/s=4m/s
所以选手摆到最低点时的速度为4m/s.
(2)选手摆到过程中,做圆周运动,设绳子对选手的拉力为F′,则在最低点时有:
F′-mg=m
解得:F′=m
+mg=60×(
+10)N=1080N
人对绳的拉力与绳对人的拉力是作用力与反作用力的关系,所以有:F=F′
则F=1080N
(3)选手从最低点开始做平抛运动
水平方向上有:x=vt
竖直方向上有:H-l=
gt2
以上两式联立解得:x=2
当l=
时,x有最大值,解得:
l=1.5m
因此,两人的看法均不正确.当绳长越接近1.5m时,落点距岸边越远.
答:(1)选手摆到最低点时的速度大小为4m/s;
(2)选手摆到最低点时对绳拉力的大小F为1080N;
(3)两人的看法均不正确.当绳长越接近1.5m时,落点距岸边越远.
| 1 |
| 2 |
代入数据解得:v=
| 2gl(1-cosα) |
| 2×10×2×(1-0.6) |
所以选手摆到最低点时的速度为4m/s.
(2)选手摆到过程中,做圆周运动,设绳子对选手的拉力为F′,则在最低点时有:
F′-mg=m
| v2 |
| l |
解得:F′=m
| v2 |
| l |
| 42 |
| 2 |
人对绳的拉力与绳对人的拉力是作用力与反作用力的关系,所以有:F=F′
则F=1080N
(3)选手从最低点开始做平抛运动
水平方向上有:x=vt
竖直方向上有:H-l=
| 1 |
| 2 |
以上两式联立解得:x=2
| l(H-l)(1-cosα) |
当l=
| H |
| 2 |
l=1.5m
因此,两人的看法均不正确.当绳长越接近1.5m时,落点距岸边越远.
答:(1)选手摆到最低点时的速度大小为4m/s;
(2)选手摆到最低点时对绳拉力的大小F为1080N;
(3)两人的看法均不正确.当绳长越接近1.5m时,落点距岸边越远.
点评:本题考查到了机械能守恒,圆周运动向心力,动能定理,平抛运动规律及求极值问题.
解答时,一定注意要求的是选手对绳子的拉力.解题过程中是对选手进行受力分析的,故不要忘记应用牛顿第三定律.应用动能定理解答时,要注意,重力做功贯穿整个过程,而浮力和阻力做功只是在水中时.关于物理当中的极值问题,要会熟练的对式子进行数学分析,从而得出结论.
解答时,一定注意要求的是选手对绳子的拉力.解题过程中是对选手进行受力分析的,故不要忘记应用牛顿第三定律.应用动能定理解答时,要注意,重力做功贯穿整个过程,而浮力和阻力做功只是在水中时.关于物理当中的极值问题,要会熟练的对式子进行数学分析,从而得出结论.

练习册系列答案
相关题目
 (2011?东城区模拟)在游乐节目中,选手需借助悬挂在高处的绳飞跃到水面的平台上,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量为m=60㎏的质点,选手抓住绳子由静止开始摆动,此时绳与竖直方向夹角α=53°,绳子的悬挂点O距水面的高度为H=3m,不考虑空气阻力和绳子的质量,平台露出水面的高度不计,水足够深.取重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6
(2011?东城区模拟)在游乐节目中,选手需借助悬挂在高处的绳飞跃到水面的平台上,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量为m=60㎏的质点,选手抓住绳子由静止开始摆动,此时绳与竖直方向夹角α=53°,绳子的悬挂点O距水面的高度为H=3m,不考虑空气阻力和绳子的质量,平台露出水面的高度不计,水足够深.取重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6 如图所示,在游乐节目中,选手需借助悬挂在高处的绳飞越到水平的浮台上.选手可视为质量m=60kg的质点,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角α=530,绳的悬挂点O距水面的高度为H=3m.不计空气阻力和绳的质量,浮台露出水面的高度不计,水足够深.g=10m/s2,sin53°=0.8,cos53°=0.6求:
如图所示,在游乐节目中,选手需借助悬挂在高处的绳飞越到水平的浮台上.选手可视为质量m=60kg的质点,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角α=530,绳的悬挂点O距水面的高度为H=3m.不计空气阻力和绳的质量,浮台露出水面的高度不计,水足够深.g=10m/s2,sin53°=0.8,cos53°=0.6求: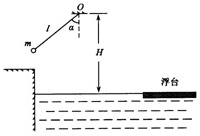 在游乐节目中,选手需借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量m=60kg的质点,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角α=53°,绳的悬挂点O距水面的高度为H=3m,绳长l不确定,不考虑空气阻力和绳的质量,浮台露出水面的高度不计.取重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.
在游乐节目中,选手需借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量m=60kg的质点,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角α=53°,绳的悬挂点O距水面的高度为H=3m,绳长l不确定,不考虑空气阻力和绳的质量,浮台露出水面的高度不计.取重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.