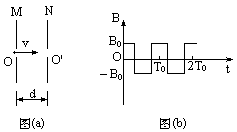
题目内容
⑴ab棒能够达到的最大速度v;
⑵ab棒速度为
 v时的加速度a;
v时的加速度a;⑶当速度为v时撤去外力F,此后棒ab能够运动的距离x。

(1) v = FR/B2l2 (2) a = F/2m,方向与F相同(3) mFR2/B4l4
⑴当安培力FA与恒力F平衡时,ab棒匀速运动,速度v达到最大
F = BIl = B2l2v/R,则v = FR/B2l2。
⑵ 速度v′= v/2时感应电动势E = Bl v′、电流强度I = E/R,安培力FA = BIl,根据牛顿第二定律有:F - FA = ma,得a = F/2m,方向与F相同。
⑶撤去F后ab在安培力作用下做减速运动,直至静止,根据在足够小的时间Δt内,有速度变化Δv,则加速度a = Δv/Δt,根据牛顿第二定律BIl = ma即B2l2v/R = ma = mΔv/Δt,变形后得到(B2l2v/R)Δt = mΔv,求和有Σ(B2l2/R)vΔt =ΣmΔv,即(B2l2/R)ΣvΔt = mv – 0;所以有(B2l2/R)x = mv,解得x = mvR/B2l2 = mFR2/B4l4。
F = BIl = B2l2v/R,则v = FR/B2l2。
⑵ 速度v′= v/2时感应电动势E = Bl v′、电流强度I = E/R,安培力FA = BIl,根据牛顿第二定律有:F - FA = ma,得a = F/2m,方向与F相同。
⑶撤去F后ab在安培力作用下做减速运动,直至静止,根据在足够小的时间Δt内,有速度变化Δv,则加速度a = Δv/Δt,根据牛顿第二定律BIl = ma即B2l2v/R = ma = mΔv/Δt,变形后得到(B2l2v/R)Δt = mΔv,求和有Σ(B2l2/R)vΔt =ΣmΔv,即(B2l2/R)ΣvΔt = mv – 0;所以有(B2l2/R)x = mv,解得x = mvR/B2l2 = mFR2/B4l4。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,直径AO垂直于水平虚线MN。一质量为m、电荷量为q的带正电小球(可视为质点)从半圆管的A点由静止滑入管内,从O点穿出后恰好通过O点正下方的C点。已知重力
,直径AO垂直于水平虚线MN。一质量为m、电荷量为q的带正电小球(可视为质点)从半圆管的A点由静止滑入管内,从O点穿出后恰好通过O点正下方的C点。已知重力 加速度为g,电场强度的大小
加速度为g,电场强度的大小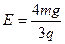 。求:
。求: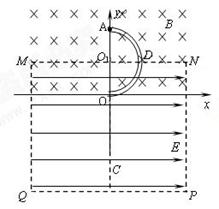
 ,半圆管对它作用力的大小;
,半圆管对它作用力的大小; 沿y轴负方向垂直射入磁场,如图所示,磁偏转后恰好沿O点水平射入电场,最后落在极板上。粒子的重力忽略不计。
沿y轴负方向垂直射入磁场,如图所示,磁偏转后恰好沿O点水平射入电场,最后落在极板上。粒子的重力忽略不计。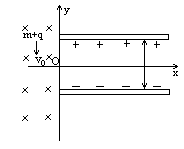

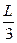

 ,且E=0,求此时粒子运动过程中距x轴的最大距离
,且E=0,求此时粒子运动过程中距x轴的最大距离 ;
; ,此时粒子运动的轨迹如图中实线所示。试求此粒子运动过程中距x轴的最大距离
,此时粒子运动的轨迹如图中实线所示。试求此粒子运动过程中距x轴的最大距离 ;
; 的2倍,试求
的2倍,试求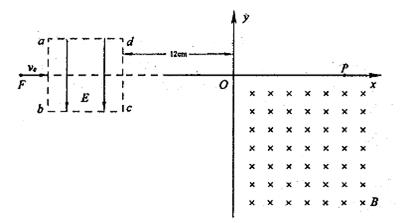

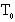 。不考虑由于磁场变化而产生的电场的影响,不计离子所受重力。求: (1)磁感强度
。不考虑由于磁场变化而产生的电场的影响,不计离子所受重力。求: (1)磁感强度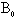 的大小。
的大小。