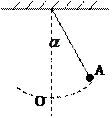题目内容
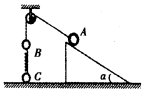
(18分)在水平地面上固定倾角为30°的光滑斜面,斜面的底端固定一个带有压力传感器的挡板P,质量均为1 kg的A、B两滑块,用劲度系数为k=100 N/m的轻弹簧相连,静止在光滑斜面上,现将另一质量为1 kg的滑块C,从斜面上某处静止释放,C滑下与B碰后粘合在一起,粘合体BC在斜面上运动的过程中,A滑块始终与P接触,当BC整体运动到斜面上最高点时,压力传感器显示压力最小值为0,g=10 m/s2,求:C刚释放时距B多远?
0.4 m
设C刚下滑时距B距离为x,即将与B碰撞时速度为v1,碰后速度大小为v2
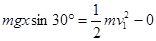 (3分)
(3分)
mv1+0=2mv2 (3分)
碰前弹簧压缩量设为x1,碰后BC整体运动到斜面上最高点时,弹簧伸长为x2,
碰前对B有mgsin30°=kx1 (2分)
碰后BC运动到最高点时对A有mgsin30°=kx2 (2分)
由以上两式得x1=x2=5×10-2m (2分)
即刚碰撞完毕时,弹簧的弹性势能与BC到达斜面上最高点时弹簧的弹性势能相等,由机械能守恒定律有
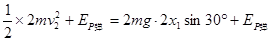 (4分)
(4分)
解得x=0.4 m. (2分)
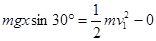 (3分)
(3分)mv1+0=2mv2 (3分)
碰前弹簧压缩量设为x1,碰后BC整体运动到斜面上最高点时,弹簧伸长为x2,
碰前对B有mgsin30°=kx1 (2分)
碰后BC运动到最高点时对A有mgsin30°=kx2 (2分)
由以上两式得x1=x2=5×10-2m (2分)
即刚碰撞完毕时,弹簧的弹性势能与BC到达斜面上最高点时弹簧的弹性势能相等,由机械能守恒定律有
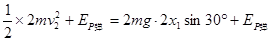 (4分)
(4分)解得x=0.4 m. (2分)

练习册系列答案
相关题目

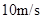 的速度沿水平方向抛出,小球经过
的速度沿水平方向抛出,小球经过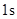 的时间落地。不计空气阻力作用。求:
的时间落地。不计空气阻力作用。求:
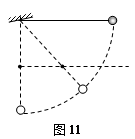

 角后,从A处无初速度释放小球,如图所示,试求:
角后,从A处无初速度释放小球,如图所示,试求: