题目内容
如图所示，质量m=2.2kg的金属块放在水平地板上，在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下，以速度v=5.0m/s向右做匀速直线运动．（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：
（1）金属块与地板间的动摩擦因数；
（2）如果从某时刻起撤去拉力，撤去拉力后金属块在水平地板上滑行的最大距离．
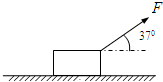
（1）金属块与地板间的动摩擦因数；
（2）如果从某时刻起撤去拉力，撤去拉力后金属块在水平地板上滑行的最大距离．
（1）因为金属块匀速运动，受力平衡则有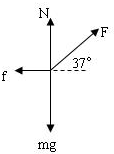
Fcos37°-μ（mg-Fsin37°）=0
得μ=
=0.5
（2）撤去外力后金属块的加速度大小为：a=μg=5m/s2
金属块在桌面上滑行的最大距离：s=
=2.5m
答：（1）金属块与地板间的动摩擦因数为0.5；
（2）如果从某时刻起撤去拉力，撤去拉力后金属块在水平地板上滑行的最大距离为2.5m．
Fcos37°-μ（mg-Fsin37°）=0
得μ=
| 8 |
| 22-6 |
（2）撤去外力后金属块的加速度大小为：a=μg=5m/s2
金属块在桌面上滑行的最大距离：s=
| v2 |
| 2a |
答：（1）金属块与地板间的动摩擦因数为0.5；
（2）如果从某时刻起撤去拉力，撤去拉力后金属块在水平地板上滑行的最大距离为2.5m．
练习册系列答案
出彩同步大试卷系列答案
相关题目
（1）在这十个连续的动作中被训航天员处于完全失重状态的时间是多少？
