题目内容
【题目】如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,动摩擦因数μ=0.2,杆的竖直部分光滑。两部分各套有质量均为lkg的小球A和B,A、B球间用不可伸缩的轻质细绳相连。初始A、B均处于静止状态,已知:OA =3m.OB =4m.若A球在水平拉力F的作用下向右缓慢地移动1m(取g=10m/s2),该过程中拉力F、摩擦力f做功分别为W1和W2,则下列答案正确的是( )
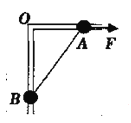
A. W1= 6 J W2=-10 J
B. W1=14J W2=-4 J
C. W1= 6 J W2=-6 J
D. W1= 4 J W2=-2 J
【答案】B
【解析】
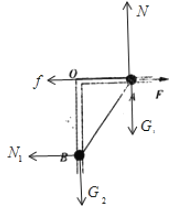
对AB整体受力分析,受拉力F、重力G、支持力N、向左的摩擦力f和向左的弹力N1
根据共点力平衡条件,有:竖直方向:N=G1+G2,水平方向:F=f+N1,其中:f=μN,解得:N=(m1+m2)g=(1+1)×10=20N,A所受的滑动摩擦力 f=μN=0.2×20N=4N,可知,f为恒力,所以摩擦力f做功![]() ,由几何关系可和在,B上升的高度为1m,所以B重力势能的增加量为
,由几何关系可和在,B上升的高度为1m,所以B重力势能的增加量为![]() ,由功能关系可得:
,由功能关系可得:![]() ,故B正确。
,故B正确。

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目