题目内容
19.利用万有引力定律可以计算天体的质量,已知万有引力常量G,下列说法正确的是( )| A. | 已知月亮绕地球做匀速圆周运动的轨道半径和周期可以计算月球质量 | |
| B. | 已知地球的半径R和地面的重力加速度g可以计算地球的质量 | |
| C. | 已知卫星绕地球做匀速圆周运动的线速度和轨道半径可以计算地球的质量 | |
| D. | 已知地球绕太阳运动的轨道半径和地球自转周期可以计算太阳的质量 |
分析 根据万有引力提供向心力,列出等式表示出中心体的质量;忽略地球自转的影响,根据万有引力等于重力列出等式表示出地球的质量.
解答 解:A、根据万有引力提供向心力得
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
M=$\frac{{{4π}^{2}r}^{3}}{{GT}^{2}}$,
已知月亮绕地球做匀速圆周运动的轨道半径和周期可以计算地球质量,不可以得出月球质量,故A错误;
B、根据地球表面的物体万有引力等于重力得
$\frac{GMm}{{{R}_{\;}}^{2}}$=mg
已知地球的半径R和地面的重力加速度g可以计算地球的质量,故B正确;
C、根据万有引力提供向心力得
$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$
M=$\frac{{v}^{2}r}{G}$,
已知卫星绕地球做匀速圆周运动的线速度和轨道半径可以计算地球的质量,故C正确;
D、根据万有引力提供向心力得
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
M=$\frac{{{4π}^{2}r}^{3}}{{GT}^{2}}$,T为公转周期,
已知地球绕太阳运动的轨道半径和地球自转周期不可以计算太阳的质量,故D错误;
故选:BC.
点评 本题考查了万有引力定律在天体中的应用,解题的关键在于找出向心力的来源,并能列出等式解题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
9.第一宇宙速度是物体在地球表面附近环绕地球做匀速圆周运动的速度,则有( )
| A. | 被发射的物体质量越大,第一宇宙速度越大 | |
| B. | 被发射的物体质量越小,第一宇宙速度越大 | |
| C. | 第一宇宙速度与被发射物体的质量无关 | |
| D. | 第一宇宙速度与地球的质量无关 |
10. 如图所示,一电子(初速度很小,可视为零)进入加速电场加速后,垂直射入偏转电场,射出后偏转位移为y,要使偏转位移增大,下列哪些措施是可行的(不考虑电子射出时碰到偏转电极板的情况)( )
如图所示,一电子(初速度很小,可视为零)进入加速电场加速后,垂直射入偏转电场,射出后偏转位移为y,要使偏转位移增大,下列哪些措施是可行的(不考虑电子射出时碰到偏转电极板的情况)( )
 如图所示,一电子(初速度很小,可视为零)进入加速电场加速后,垂直射入偏转电场,射出后偏转位移为y,要使偏转位移增大,下列哪些措施是可行的(不考虑电子射出时碰到偏转电极板的情况)( )
如图所示,一电子(初速度很小,可视为零)进入加速电场加速后,垂直射入偏转电场,射出后偏转位移为y,要使偏转位移增大,下列哪些措施是可行的(不考虑电子射出时碰到偏转电极板的情况)( )| A. | 增大偏转电压U | B. | 减小加速电压U0 | ||
| C. | 增大极板间距离 | D. | 将电子改成负离子 |
14.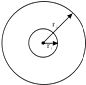 两颗绕地球做匀速圆周运动的人造地球卫星,如图所示,它们的质量之比为2:1,到地球球心的距离之比为1:3,则它们的( )
两颗绕地球做匀速圆周运动的人造地球卫星,如图所示,它们的质量之比为2:1,到地球球心的距离之比为1:3,则它们的( )
 两颗绕地球做匀速圆周运动的人造地球卫星,如图所示,它们的质量之比为2:1,到地球球心的距离之比为1:3,则它们的( )
两颗绕地球做匀速圆周运动的人造地球卫星,如图所示,它们的质量之比为2:1,到地球球心的距离之比为1:3,则它们的( )| A. | 周期之比为3:1 | B. | 线速度之比为1:3 | ||
| C. | 向心加速度之比为1:9 | D. | 向心力之比为18:1 |
11. 两个大小相同的小球带有同种电荷,质量分别为m1和m2,带电荷量分别是q1和q2,用绝缘线悬挂后,因静电力而使两悬线张开,分别与中垂线方向成α1角和α2角,且两球处于同一水平线上,如图所示,若α1=α2,则下述结论正确的是( )
两个大小相同的小球带有同种电荷,质量分别为m1和m2,带电荷量分别是q1和q2,用绝缘线悬挂后,因静电力而使两悬线张开,分别与中垂线方向成α1角和α2角,且两球处于同一水平线上,如图所示,若α1=α2,则下述结论正确的是( )
 两个大小相同的小球带有同种电荷,质量分别为m1和m2,带电荷量分别是q1和q2,用绝缘线悬挂后,因静电力而使两悬线张开,分别与中垂线方向成α1角和α2角,且两球处于同一水平线上,如图所示,若α1=α2,则下述结论正确的是( )
两个大小相同的小球带有同种电荷,质量分别为m1和m2,带电荷量分别是q1和q2,用绝缘线悬挂后,因静电力而使两悬线张开,分别与中垂线方向成α1角和α2角,且两球处于同一水平线上,如图所示,若α1=α2,则下述结论正确的是( )| A. | q1一定等于q2 | B. | 一定满足$\frac{{q}_{1}}{{m}_{1}}$=$\frac{{q}_{2}}{{m}_{2}}$ | ||
| C. | m1一定等于m2 | D. | 必须同时满足q1=q2、m1=m2 |
9. 如图所示,在光滑的水平面上有一个小球a以初速度v0向右运动,与此同时,在它的正上方有一个小球b也以v0的初速度水平向右抛出,并落于水平面的c点,则( )
如图所示,在光滑的水平面上有一个小球a以初速度v0向右运动,与此同时,在它的正上方有一个小球b也以v0的初速度水平向右抛出,并落于水平面的c点,则( )
 如图所示,在光滑的水平面上有一个小球a以初速度v0向右运动,与此同时,在它的正上方有一个小球b也以v0的初速度水平向右抛出,并落于水平面的c点,则( )
如图所示,在光滑的水平面上有一个小球a以初速度v0向右运动,与此同时,在它的正上方有一个小球b也以v0的初速度水平向右抛出,并落于水平面的c点,则( )| A. | 小球a先到达c点 | B. | 小球b先到达c点 | C. | 两球同时到达c点 | D. | 不能确定 |
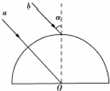 如图所示为一半球形介质的截面,O为圆心,a、b两束平行红色光从不同位置进入介质,已知介质的折射率为$\sqrt{2}$,球半径为R,光线a沿半径方向入射且在O点恰好发生全反射,光在真空中的传播速度为c,求:
如图所示为一半球形介质的截面,O为圆心,a、b两束平行红色光从不同位置进入介质,已知介质的折射率为$\sqrt{2}$,球半径为R,光线a沿半径方向入射且在O点恰好发生全反射,光在真空中的传播速度为c,求: