题目内容
15.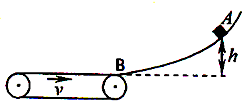 如图所示,足够长的水平传送带以速度v=2m/s沿顺时针方向运动,传送带的右端与光滑曲面的底部在B点平滑连接,曲面上的A点距离底部的高度为h=0.45m.一质量m=1kg的小物块从A点静止滑下,经B点滑上传送带,小物块与传送带间的动摩擦因数为μ=0.2,经过一段时间后小物块又再次返回B点,求:
如图所示,足够长的水平传送带以速度v=2m/s沿顺时针方向运动,传送带的右端与光滑曲面的底部在B点平滑连接,曲面上的A点距离底部的高度为h=0.45m.一质量m=1kg的小物块从A点静止滑下,经B点滑上传送带,小物块与传送带间的动摩擦因数为μ=0.2,经过一段时间后小物块又再次返回B点,求:(1)第一次经过B点的速度v1大小(取g=10m/s2);
(2)从第一次经过B点到再次返回B点过程中产生的热量Q.
分析 (1)根据机械能守恒定律求出滑块滑上传送带的速度,;
(2)根据动能定理通过物体的初末速度,求出物体从第一次滑上传送带到离开传送带的过程中,传送带对物体做的功.根据运动学公式求出相对路程的大小,从而根据Q=f△x求出摩擦产生的热量.
解答 解:(1)物体沿圆弧轨道下滑过程中机械能守恒,设物体滑到传送带底端时的速度为v1,则有:
mgR=$\frac{1}{2}$mv12,
代入数据得:v1=3 m/s
(2)小物块由B向左匀减速到速度变为零,再反向匀加速到与皮带速度相等,最后匀速运动回B点,故v2=2m/s
小物块在皮带上运动的加速度大小为a,则:μmg=ma
所以:a=μg=0.2×10=2m/s2
小物块向左匀减速的时间为t1:${t}_{1}=\frac{0-{v}_{1}}{-a}=\frac{0-3}{-2}=1.5$s
小物块向右匀加速的时间为:${t}_{2}=\frac{v}{a}=\frac{2}{2}=1$s
两段过程中,小物块相对于传送带的位移:$△x=v({t}_{1}+{t}_{2})+\frac{{v}_{1}^{2}}{2a}-\frac{1}{2}a{t}_{2}^{2}$
产生的热量为:Q=μmg△x
代入数据,联立解得:Q=12.5J
答:(1)第一次经过B点的速度v1大小是3m/s;
(2)从第一次经过B点到再次返回B点过程中产生的热量是12.5J.
点评 解决本题的关键理清物体的运动过程,知道物体的运动规律,结合动能定理、牛顿第二定律和运动学公式进行求解.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
5. 一皮带传动装置,轮A、B均沿同方向转动,设皮带不打滑,a、b为两轮边缘上的点,某时刻a、b、o、o′位于同一水平面上,如图所示.设该时刻a、b所受摩擦力分别为fa、fb,则下列说法正确的是( )
一皮带传动装置,轮A、B均沿同方向转动,设皮带不打滑,a、b为两轮边缘上的点,某时刻a、b、o、o′位于同一水平面上,如图所示.设该时刻a、b所受摩擦力分别为fa、fb,则下列说法正确的是( )
 一皮带传动装置,轮A、B均沿同方向转动,设皮带不打滑,a、b为两轮边缘上的点,某时刻a、b、o、o′位于同一水平面上,如图所示.设该时刻a、b所受摩擦力分别为fa、fb,则下列说法正确的是( )
一皮带传动装置,轮A、B均沿同方向转动,设皮带不打滑,a、b为两轮边缘上的点,某时刻a、b、o、o′位于同一水平面上,如图所示.设该时刻a、b所受摩擦力分别为fa、fb,则下列说法正确的是( )| A. | fa、fb都是动力、而且方向相同 | |
| B. | fa、fb都是阻力,而且方向相反 | |
| C. | fa若是动力,则fb一定是阻力,两力方向相反 | |
| D. | fa若是阻力,则fb一定是动力,两方向相同 |
10.物体做匀加速直线运动,已知加速度为3m/s2,那么任意1秒时间内( )
| A. | 物体的末速度一定等于初速度的3倍 | |
| B. | 物体的末速度一定比初速度大3m/s | |
| C. | 第5s的初速度一定比第4s的末速度大3m/s | |
| D. | 第5s的初速度一定比第4s的初速度大3m/s |
20.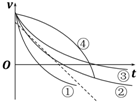 以不同初速度将两个物体同时竖直上抛并开始计时,用虚线和实线①②③④分别描述一个物体所受空气阻力可忽略和另一物体所受空气阻力大小与物体速率成正比的v-t图象如图所示,下列实线中正确的可能是( )
以不同初速度将两个物体同时竖直上抛并开始计时,用虚线和实线①②③④分别描述一个物体所受空气阻力可忽略和另一物体所受空气阻力大小与物体速率成正比的v-t图象如图所示,下列实线中正确的可能是( )
 以不同初速度将两个物体同时竖直上抛并开始计时,用虚线和实线①②③④分别描述一个物体所受空气阻力可忽略和另一物体所受空气阻力大小与物体速率成正比的v-t图象如图所示,下列实线中正确的可能是( )
以不同初速度将两个物体同时竖直上抛并开始计时,用虚线和实线①②③④分别描述一个物体所受空气阻力可忽略和另一物体所受空气阻力大小与物体速率成正比的v-t图象如图所示,下列实线中正确的可能是( )| A. | 图线① | B. | 图线② | C. | 图线③ | D. | 图线④ |
4. 如图所示,沿同一直线运动的物体A、B,其相对于同一参考系的位置x随时间变化的函数图象可知( )
如图所示,沿同一直线运动的物体A、B,其相对于同一参考系的位置x随时间变化的函数图象可知( )
 如图所示,沿同一直线运动的物体A、B,其相对于同一参考系的位置x随时间变化的函数图象可知( )
如图所示,沿同一直线运动的物体A、B,其相对于同一参考系的位置x随时间变化的函数图象可知( )| A. | 、从第2秒起,两物体运动方向相反,且vA>vB | |
| B. | 、两物体从同一位置开始运动,但A物体比B物体迟2s才开始运动 | |
| C. | 、在3s内两物体位移方向相反,3s末A、B相遇 | |
| D. | 、3s末两物体速度大小相等 |
4. 如图所示两个带等量正电荷的点电荷,O点为两电荷连线的中点,a点在连线的中垂线上,若在a点由静止释放一个电子,只在静电力的作用下,关于电子的运动,下列说法正确的是( )
如图所示两个带等量正电荷的点电荷,O点为两电荷连线的中点,a点在连线的中垂线上,若在a点由静止释放一个电子,只在静电力的作用下,关于电子的运动,下列说法正确的是( )
 如图所示两个带等量正电荷的点电荷,O点为两电荷连线的中点,a点在连线的中垂线上,若在a点由静止释放一个电子,只在静电力的作用下,关于电子的运动,下列说法正确的是( )
如图所示两个带等量正电荷的点电荷,O点为两电荷连线的中点,a点在连线的中垂线上,若在a点由静止释放一个电子,只在静电力的作用下,关于电子的运动,下列说法正确的是( )| A. | 电子在从a向O运动的过程中,加速度一定越来越大,速度一定越来越大 | |
| B. | 电子在从a向O运动的过程中,加速度可能越来越小,速度一定越来越大 | |
| C. | 电子运动到O时,加速度为零,速度最大 | |
| D. | 电子通过O后,加速度可能先增大后减小,速度一定越来越小,一直到速度为零 |
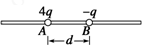 如图所示,带电荷量分别为4q和-q的小球A、B固定在水平放置的光滑绝缘细杆上,相距为d.带电体均可视为点电荷.试求:
如图所示,带电荷量分别为4q和-q的小球A、B固定在水平放置的光滑绝缘细杆上,相距为d.带电体均可视为点电荷.试求:
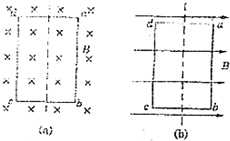 如图所示,矩形线圈由100匝组成,ab边长L1=0.40m,ad边长L2=0.20m,在B=0.1T的匀强磁场中,以两短边中点的连线为轴转动,转速n′=50r/s.求:
如图所示,矩形线圈由100匝组成,ab边长L1=0.40m,ad边长L2=0.20m,在B=0.1T的匀强磁场中,以两短边中点的连线为轴转动,转速n′=50r/s.求: