题目内容
如图所示，倾角为37°，长度为d的光滑绝缘斜面上，一个带电的小物体质量为m，带电量为q，置于斜面顶端．当沿水平向右加一个如图所示的匀强电场时，木块恰好静止在斜面上．从某时开始，匀强电场的电场强度突然减小为原来的| 1 | 3 |
（1）物体带哪种电．
（2）原来的电场强度．
（3）带电物体滑到斜面底端时速率．（已知重力加速度为g）
分析：（1）对物体受力分析，通过电场力的方向确定物体的电性．
（2）根据共点力平衡求出电场力的大小，从而得出电场强度的大小．
（3）根据牛顿第二定律求出带电物体的加速度，结合速度位移公式求出带电物体滑到斜面底端时速率．
（2）根据共点力平衡求出电场力的大小，从而得出电场强度的大小．
（3）根据牛顿第二定律求出带电物体的加速度，结合速度位移公式求出带电物体滑到斜面底端时速率．
解答：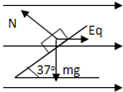
解：（1）根据共点力平衡知，物体所受的电场力水平向右，则物体带正电．
（2）根据共点力平衡得，qE=mgtan37°
解得E=
=
．
（3）匀强电场的电场强度突然减小为原来的
，根据牛顿第二定律得，
a=
=0.4g．
根据v2=2ad得，v=
=
．
答：（1）物体带正电．
（2）原来的电场强度为
．
（3）带电物体滑到斜面底端时速率为
．
解：（1）根据共点力平衡知，物体所受的电场力水平向右，则物体带正电．（2）根据共点力平衡得，qE=mgtan37°
解得E=
| mgtan37° |
| q |
| 3mg |
| 4q |
（3）匀强电场的电场强度突然减小为原来的
| 1 |
| 3 |
a=
mgsin37°-q
| ||
| m |
根据v2=2ad得，v=
| 2ad |
| 0.8gd |
答：（1）物体带正电．
（2）原来的电场强度为
| 3mg |
| 4q |
（3）带电物体滑到斜面底端时速率为
| 0.8gd |
点评：解决本题的关键能够正确地受力分析，运用共点力平衡和牛顿第二定律进行求解，知道加速度是联系力学和运动学的桥梁．
练习册系列答案
百年学典课时学练测系列答案
相关题目
如图所示，倾角为37°斜面上方有一小球以一定的速度水平抛出，在空中飞行2s后恰好垂直撞在斜面上，sin37°=0.6，cos37°=0.8，g=10m/s2．求：
如图所示，倾角为37°、足够长的斜面体固定在水平地面上，小木块在沿斜面向上的恒定外力F作用下，从斜面上的A点由静止开始向上作匀加速运动，前进了4.0m抵达B点时，速度为8m/s．已知木块与斜面间的动摩擦因数μ=0.5，木块质量m=1kg．g取10m/s2，sin37°=0.6，cos37°=0.8．
如图所示，倾角为37°的粗糙斜面的底端有一质量m=1kg的凹形小滑块，小滑块与斜面间的动摩擦因数μ=0.25．现小滑块以某一初速度v从斜面底端上滑，同时在斜面底端正上方有一小球以v0水平抛出，经过0.4s，小球恰好垂直斜面方向落入凹槽，此时，小滑块还在上滑过程中．（已知sin37°=0.6，cos37°=0.8），g取10m/s2，求：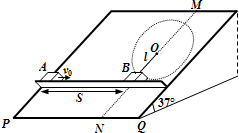
如图所示，倾角为37°的足够大斜面以直线MN为界由两部分组成，MN垂直于斜面水平底边PQ且其左边光滑右边粗糙，斜面上固定一个既垂直于斜面又垂直于MN的粗糙挡板．质量为m1=3kg的小物块A置于挡板与斜面间，A与挡板间的动摩擦因数为μ1=0.1．质量为m2=1kg的小物块B用不可伸长的细线悬挂在界线MN上的O点，细线长为l=0.5m，此时，细线恰好处于伸直状态．A、B可视为质点且与斜面粗糙部分的动摩擦因数均为μ2=0.3，它们的水平距离S=7.5m．现A以水平初速v0=5m/s向右滑动并恰能与B发生弹性正撞．g=10m/s2．求：
如图所示，倾角为θ=37°的斜面固定在水平桌面上，劲度系数为200N/m的轻质弹簧上端固定在斜面顶端的木板上，下端连接孩子两位1kg的物块A，弹簧与斜面平行；物块A的下面用跨过光滑定滑轮的轻绳连接质量为0.15kg的物块B，物块A与滑轮之间的轻绳平行于斜面；B的下面用轻绳连接质量为0.95kg的物块C．此时弹簧的伸长量为6cm，整个装置处于静止状态．取g=10m/s2，sin37°=0.6．则下列说法中正确的是（ ）| A、物块A受到6个作用力 | B、物块A受到的摩擦力方向沿斜面向上，大小为5N | C、剪断B、C间轻绳后，物块A收到的摩擦力方向沿斜面向下 | D、剪断A、B间轻绳后，物块A一定沿斜面向上运动 |