题目内容
【题目】如图所示,圆心角θ=60°的圆弧轨道JK与半圆弧轨道GH都固定在竖直平面内,在两者之间的光滑地面上放置质量为M的木板,木板上表面与H、K两点相切,木板右端与K端接触,左端与H点相距L,木板长度d=6.5R。两圆弧轨道均光滑,半径为R。现在相对于J点高度为3R的P点水平向右抛出一可视为质点的质量为m的木块,木块恰好从J点沿切线进入圆弧轨道,然后滑上木板,木块与 木板间的动摩擦因数![]() ;当木板接触H点时即被黏住,木块恰好能运动到半圆弧轨道GH的中点。已知M=2m,重力加速度为g。
;当木板接触H点时即被黏住,木块恰好能运动到半圆弧轨道GH的中点。已知M=2m,重力加速度为g。

(1)求木块在P点抛出的初速度大小以及运动到K时对K点的压力;
(2)求L的大小(结果用字母m、g、R表示)
【答案】(1) ![]() ;
; ![]() (2)
(2) ![]()
【解析】试题分析:物块从P到J做平抛运动,根据下落的高度求出平抛运动的时间,由vy=gt求出滑块到达J点的竖直分速度,由分速度关系求平抛的初速度;P到K根据机械能守恒定律可以求出滑块到达K点的速度,然后应用牛顿第二定律求出支持力;物块从滑上滑板后开始做匀减速运动,此时滑板开始做匀加速直线运动,当物块与滑板达到共同速度时,二者开始做匀速运动.根据动量守恒定律求出共同速度,再由能量守恒定律求L。
(1)设木块在P点的初速度为v1,从P点到J点做平抛运动
竖直方向有: ![]()
竖直方向的速度为:![]()
因为木块在J点与圆弧相切,故![]()
联立解得:![]()
(2)设木块滑到K点的速度为![]() ,从P点到K点根据机械能守恒定律有
,从P点到K点根据机械能守恒定律有![]()
解得:![]()
根据牛顿第二定律可得:![]()
解得:![]()
根据牛顿第三定律可得木块运动到K时,对K点的压力为10mg,方向竖直向下
(2)木块从K点滑上木板后开始做匀减速运动,此时木板开始做匀加速直线运动,假设木块与木板能达到共同速度![]() ,则此后二者开始做匀速运动,规定
,则此后二者开始做匀速运动,规定![]() 的方向为正方向,
的方向为正方向,
根据动量守恒定律可得:![]()
解得:![]()
对木块根据动能定理有:![]()
对木板根据动能定理有:![]()
解得![]() ,
,
木块相对木板的位移:![]()
即木板与木块到达相同速度时,木块未离开木板
设木块运动到H点时速度大小为![]() ,根据动能定理可得
,根据动能定理可得![]()
解得: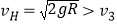
说明两者还未达到共速,木板的左端即与H点粘连,木块从K点到H点一直受到摩擦阻力作用,则由动能定理可得![]()
解得:L=0.5R。