题目内容
【题目】如图所示,在同一竖直平面内,一轻质弹簧一端固定,另一自由端恰好与水平线CB平齐,B、C两点间水平距离S=30cm,静止放在倾角为53°的光滑斜面上.一质量为m=1kg的小球从高度h=20 cm平台边缘A点以某一速度水平抛出,之后小球在运动过程中恰好沿斜面方向将弹簧压缩,最大压缩量为x=5 cm.(g=10 m/s2,sin 53°=0.8,cos 53°=0.6)求:
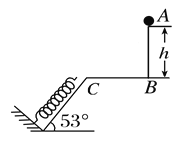
(1)小球从A点抛出时速度vA为多大?
(2)弹簧所获得的最大弹性势能Ep为多大?
(保留两位有效数字)
【答案】(1)1.5m/s (2)3.5J
【解析】试题分析:小球离开平台后做平抛运动,列出竖直和水平运动公式即可解得小球从A点抛出时速度;根据速度关系求出C点的速度,在根据根据机械能守恒定律可得弹簧所获得的最大弹性势能Ep。
(1)小球离开平台后做平抛运动
在竖直方向: ![]()
水平方向: ![]()
代入数据解得:![]()
(2)由题意可知速度间的关系为: ![]()
代入数据解得:![]()
弹簧和小球组成系统从C处到弹簧压缩最大的过程中,根据机械能守恒定律有: ![]()
代入数据解得EP=3.5J

练习册系列答案
相关题目