Question

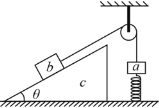
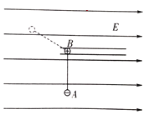
【题目】如图所示，长为l的绝缘轻杆两端连接A、B两小球，其质量分别为m1、m2,带电量分别为-q、+q。将小球B置于水平光滑绝缘轨道内并固定，整个个装置处于水平向右的匀强电场中，轻杆从图中竖直位置由静止释放，可绕小球B无摩擦转动，顺时针转过的最大角度为127°(sin37°=0.6，cos37°=0.8)

（1）求匀强电场的场强大小E；

（2）当轻杆转过90°时，求杆对A球的作用力的大小（不计A、B球间的库仑力)；

（3）若解除固定，小球B在轨道内可自由移动，轻杆仍从图中竖直位置由静止释放，当轻杆转过90°时，求小球A的速度大小（水平轨道对轻杆和小球A的运动无影响）。

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）根据动能定理得

代入数据解得匀强电场的场强大小

（2）当轻杆转过90°时，根据动能定理得

解得

根据牛顿第二定律得

解得杆对A球的作用力的大小

（3）设轻杆转过90°时，A球的水平速度为，竖直速度为，B球的速度为

由AB系统水平方向上动量守恒

因为杆不可伸长，可得

A、B能量守恒

解得