题目内容
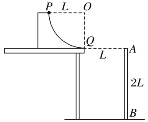
【题目】探究平抛运动实验装置如图所示，半径为 L 的四分之一圆轨道(可视为光滑) 固定于水平桌面上，切口水平且与桌边对齐，切口离地面高度为 2L.离切口水平距离为 L 的一探测屏 AB 竖直放置，一端放在水平面上，其高为 2L.一质量为 m 的小球从圆轨道上不同的位置静止释放打在探测屏上．若小球在运动过程中空气阻力不计，小球可视为质点， 重力加速度为 g.求：
(1)小球从图示位置 P 处静止释放，到达圆轨道最低点 Q 处速度大小及小球对圆轨道压力；
(2)为让小球能打在探测屏上，小球应从圆轨道上什么范围内静止释放？
(3)小球从什么位置静止释放，小球打在屏上时动能最小，最小动能为多少？
【答案】(1)3mg,方向竖直向下(2) 
(3) 
【解析】
(1)小球从P处下滑到Q点，由机械能守恒可得：
得：v= 
在Q点对小球受力分析得：
代入得：FN=3mg
根据牛顿第三定律，小球对轨道压力大小为3mg，方向竖直向下。
(2)小球从轨道上某点C下滑到Q处平拋，恰好打在B点，则根据平拋运动规律
竖直方向2L= 
，
水平方向vQ=L/t
从C到Q根据机械能守恒得：
mghc= 
得：hc=L/8
即小球从PC范围内从静止释放均能打到探测屏上。
(3)设从Q处以速度v0射出，打到探测屏上，其动能为：
Ek= 
+mgh
而h==g2(Lv0)2
L=v0t
得Ek=+
由数学知识得v0=
时Ek最小，且Ekmin=mgL
释放点位置离Q的竖直高度H=L/2
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
